Question 1125874: A women bought a number of items for $48. She realizes that if she bought 6 more items for the same money, she would have paid $4 less per item. How many items did she buy?
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13209)   (Show Source): (Show Source):
Answer by ikleyn(52879)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The original formulation in the post is TERRIBLE (from the common sense of view).
And it is the main reason why the problem seems to be upside-down, staying on the head.
So the first step is to transform it to the right form.
Much more reasonable (classic form) formulation (after editing) is this:
A women bought a number of equally priced items for $48. Had the price be $4 less for each item, she could buy 6 more items
for the same money. How many items did she buy?
In this formulation, the standard algebra solution is and works as follows.
x*p = 48, (1)
(x+6)*(p-4) = 48. (2)
Simplify equation (2) :
xp + 6p - 4x - 24 = 48.
Replace the term xp in the left side of the last equation by 48, based on (1) :
48 + 6p - 4x - 24 = 48,
6p - 4x = 24. (3)
From equation (3), express p = 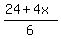 and substitute it into equation (1). You will get and substitute it into equation (1). You will get
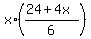 = 48,
x*(24+4x) = 288
4x^2 +24x - 288 = 0
x^2 + 6x - 72 = 0
(x+12)*(x-6) = 72.
The positive root (which only makes sense) is 6.
Answer. The women bought 6 items. = 48,
x*(24+4x) = 288
4x^2 +24x - 288 = 0
x^2 + 6x - 72 = 0
(x+12)*(x-6) = 72.
The positive root (which only makes sense) is 6.
Answer. The women bought 6 items.
Solved.
------------------
Was it so ugly ?
But of course, not - if you know on how to do it in a correct way.
Simply a standard (and a smooth) algebra solution, and you should learn on how to solve it algebraically -
simply because you can meet many of such problems in your student years.
To see many other similar solved problems, look into the lesson
- Had they sold . . .
in this site.
|
|
|