Question 1111276: Find the minimum slope of the line tangent to the curve y = x³-3x²+6x+3.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The slope of the line tangent to the curve 
for each value of  is the value of the derivative, is the value of the derivative,
 . .

 is a quadratic polynomial and graphs as a parabola. is a quadratic polynomial and graphs as a parabola.
You are asked for the minimum value of that expression,
and there are several ways to get to the result.
Can you figure out what way your teacher would favor?
Maybe your teacher expects you to find the minimum of
 by looking at by looking at
zeros and changes of sign of  . .
As 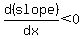 for for  , ,
 for for  , and , and
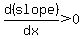 for for 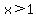 , ,
there is a minimum at  . .
The minimum slope, for  is is
 . .
Alternately, if you memorized class information,
you know that the expression  with with 
has a minimum at  . .
Maybe your teacher expects you to do that,
find that the minimum is at  , ,
and calculate that for  , ,
 . .
You could just use your algebra knowledge (no memorization)
and "complete the square" like this






As  , , 
|
|
|