Question 1105686: at what time after 4 pm will the 6 o'clock mark bisect the angle formed by the minute and the hour hand?
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13200)   (Show Source): (Show Source):
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
at what time after 4pm will the 6 o'clock mark bisect the angle formed by the minute and the hour hand?
~~~~~~~~~~~~~~~~~~~~~~~
If you give yourself the labor to think 1-2-3 minutes on the problem before to start solving it, you will get understanding that
the problem has MANY (much more than one) solutions:
1. One solution when the hour hand is between 4 and 5 hour marks;
2. 2-nd solution when the hour hand is between 5 and 6 hour marks;
3. 3-rd solution when the hour hand is between 6 and 7 hour marks;
4. 4-th solution when the hour hand is between 7 and 8 hour marks;
5. 5-th solution when the hour hand is between 8 and 9 hour marks;
6. 6-th solution when the hour hand is between 9 and 10 hour marks;
7. 7-th solution when the hour hand is between 10 and 11 hour marks;
8. 8-th solution when the hour hand is between 11 and 12 hour marks.
- - - I can even continue FURTHER, but think it is enough. - - -
Let me recall you that the angular rate of the minute hand is 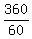 = 6 degrees per minute, and
angular rate of the hour hand is = 6 degrees per minute, and
angular rate of the hour hand is  = 30 degrees per hour, or 0.5 degrees per minute.
We will count the positions of the hour hand and the minute hand starting from their positions "vertically up" at the noon.
Also, I will use hAngle for the angle position of the hour hand, and mAngle for the angle position of the minute hand.
1. Case 1), solved by @greenestamps, when the hour hand is between 4 and 5 hour marks.
In this case, x minutes after 4 o'clock (0<=x<=60),
hour hand is in position 120 + 0.5x degrees, while the minute hand is in position 6x.
The equation is hAngle + mAngle = 360 degrees, or
120 + 0.5x + 6x = 360 with the solution x = = 30 degrees per hour, or 0.5 degrees per minute.
We will count the positions of the hour hand and the minute hand starting from their positions "vertically up" at the noon.
Also, I will use hAngle for the angle position of the hour hand, and mAngle for the angle position of the minute hand.
1. Case 1), solved by @greenestamps, when the hour hand is between 4 and 5 hour marks.
In this case, x minutes after 4 o'clock (0<=x<=60),
hour hand is in position 120 + 0.5x degrees, while the minute hand is in position 6x.
The equation is hAngle + mAngle = 360 degrees, or
120 + 0.5x + 6x = 360 with the solution x = 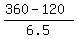 = 36.923 minutes (approximately).
The answer is: 4 hours and 36.923 minutes PM (approximately).
2. Case 2), when the hour hand is between 5 and 6 hour marks.
In this case, x minutes after 5 o'clock (0<=x<=60),
hour hand is in position 150 + 0.5x degrees, while the minute hand is in position 6x.
The equation is hAngle + mAngle = 360 degrees, or
150 + 0.5x + 6x = 360 with the solution x = = 36.923 minutes (approximately).
The answer is: 4 hours and 36.923 minutes PM (approximately).
2. Case 2), when the hour hand is between 5 and 6 hour marks.
In this case, x minutes after 5 o'clock (0<=x<=60),
hour hand is in position 150 + 0.5x degrees, while the minute hand is in position 6x.
The equation is hAngle + mAngle = 360 degrees, or
150 + 0.5x + 6x = 360 with the solution x = 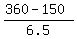 = 32.308 minutes (approximately).
The answer is: 5 hours and 32.308 minutes PM (approximately).
3. Case 3), when the hour hand is between 6 and 7 hour marks.
In this case, x minutes after 6 o'clock (0<=x<=60),
hour hand is in position 180 + 0.5x degrees, while the minute hand is in position 6x.
The equation is hAngle + mAngle = 360 degrees, or
180 + 0.5x + 6x = 360 with the solution x = = 32.308 minutes (approximately).
The answer is: 5 hours and 32.308 minutes PM (approximately).
3. Case 3), when the hour hand is between 6 and 7 hour marks.
In this case, x minutes after 6 o'clock (0<=x<=60),
hour hand is in position 180 + 0.5x degrees, while the minute hand is in position 6x.
The equation is hAngle + mAngle = 360 degrees, or
180 + 0.5x + 6x = 360 with the solution x = 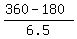 = 27.692 minutes (approximately).
The answer is: 6 hours and 27.692 minutes PM (approximately).
4. Case 4), when the hour hand is between 7 and 8 hour marks.
In this case, x minutes after 7 o'clock (0<=x<=60),
hour hand is in position 210 + 0.5x degrees, while the minute hand is in position 6x.
The equation is hAngle + mAngle = 360 degrees, or
210 + 0.5x + 6x = 360 with the solution x = = 27.692 minutes (approximately).
The answer is: 6 hours and 27.692 minutes PM (approximately).
4. Case 4), when the hour hand is between 7 and 8 hour marks.
In this case, x minutes after 7 o'clock (0<=x<=60),
hour hand is in position 210 + 0.5x degrees, while the minute hand is in position 6x.
The equation is hAngle + mAngle = 360 degrees, or
210 + 0.5x + 6x = 360 with the solution x = 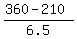 = 23.077 minutes (approximately).
The answer is: 7 hours and 27.692 minutes PM (approximately). = 23.077 minutes (approximately).
The answer is: 7 hours and 27.692 minutes PM (approximately).
And so on . . .
You can do next steps and solve next cases on your own . . .
-----------------
You can find many solved clock problems in the lessons
- Clock problems
- Advanced clock problems
- Gaining clock problem
in this site.
Clock problems are very attractive and bring a lot of fun (as well as are very educative, too),
so do not miss an opportunity/(a chance) to get acquainted with their solutions.
|
|
|