SOLUTION: if the price of eggs rises 10 cents per dozen one will be able to get 2 dozen fewer eggs with 6$ that was possible at a lower price. what was the lower price?

Algebra ->  Customizable Word Problem Solvers  -> Misc -> SOLUTION: if the price of eggs rises 10 cents per dozen one will be able to get 2 dozen fewer eggs with 6$ that was possible at a lower price. what was the lower price?      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 1101202: if the price of eggs rises 10 cents per dozen one will be able to get 2 dozen fewer eggs with 6$ that was possible at a lower price. what was the lower price?
Answer by ikleyn(52775) About Me  (Show Source):
You can put this solution on YOUR website!
.
Let L be the lower price per dozen of eggs, in dollars (which is under the question).

Then the new price is (L+0.1) dollars per dozen.      (Notice 0.1 = 0.1 dollars = 10 cents)


At the lower price, the buyer could buy 6%2FL dozens for 6 dollars.


At the new price, it can buy only 6%2F%28L%2B0.1%29 dozens.


The condition says that this difference is 2 dozens:

6%2FL - 6%2F%28L%2B0.1%29 = 2.


To solve this equation, multiply both sides by L*(L+0.1). You will get

6*(L+0.1) - 6L = 2*L*(L+0.1).


Simplify it step by step:

6L + 0.6 - 6L = 2L^2 + 0.2L,

0.6 = 2L^2 + 0.2L  ====>  2L^2 + 0.2L - 0.6 = 0  ====>  divide by 2 both sides  ====>

L^2 + 0.1L - 0.3 = 0

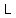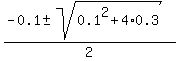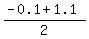L%7B1%2C2%5D = %28-0.1+%2B-+sqrt%280.1%5E2+%2B+4%2A0.3%29%29%2F2 = %28-0.1+%2B-+1.1%29%2F2.


The only positive root is  L = %28-0.1+%2B+1.1%29%2F2 = 0.5.


Answer.  The lower price was $0.5 per dozen of eggs.


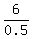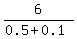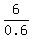Check.   6%2F0.5 = 12;   6%2F%280.5%2B0.1%29 = 6%2F0.6 = 10;   12 - 10 = 2   ! Correct !

Solved.