Question 1099035: two numbers are in the ratio 2 to 7 and their product is 126. what is the larger number?
Found 3 solutions by KMST, ikleyn, MathTherapy:
Answer by KMST(5328)   (Show Source):
Answer by ikleyn(52776)  (Show Source):
You can put this solution on YOUR website! .
You may consider another logic/solution.
If the numbers are in the ratio 2 to 7, it means that one number is 2x, while another number is 7x, where x is an unknown factor.
Then the product of these numbers is (2x)*(7x) = 14x^2.
At the same time, the product is 126, according to the condition.
It gives you an equation 14x^2 = 126.
Hence, x^2 = 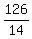 = 9.
It implies x = +/-  = +/- 3.
If x = 3, then your answer is: the two numbers are 2*3 = 6 and 7*3 = 21.
The greatest of the two numbers is 21.
If x = -3, then your answer is: the two numbers are 2*(-3) = -6 and 7*(-3) = -21.
In this case the greatest of the two numbers is -6.
Answer. There are two answers to the problem's question: -6 and 21.
Answer by MathTherapy(10551)  (Show Source):
|
|
|
