The number of chocolate chips in an 18-ounce bag of chocolate chip cookies is approximately normally distributed with a mean of 1252 chips and standard deviation 129 chips.
(a) What is the probability that a randomly selected bag contains between 1000
and 1500 chocolate chips, inclusive?
(b) What is the probability that a randomly selected bag contains fewer than 1050
chocolate chips?
(c) What proportion of bags contains more than 1175
chocolate chips?
(d) What is the percentile rank of a bag that contains 1450
chocolate chips?
I am so confused. Please help me :(
How are you supposed to do this? Are you supposed to do it manually, or use the TI-83/84 calculator?
Let me START you off/Get you going with a)
MANUALLY
Determine probability of SMALLER VALUE (1,000, in this case)
Using:  , where:
, where:  = 1,000
= 1,000
 = 1,252
= 1,252
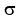 = 129
= 129
 then becomes:
then becomes:  A Z-score of - 1.95 = .0256
Determine probability of LARGER VALUE (1,500, in this case)
Using:
A Z-score of - 1.95 = .0256
Determine probability of LARGER VALUE (1,500, in this case)
Using:  , where:
, where:  = 1,500
= 1,500
 = 1,252
= 1,252
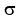 = 129
= 129
 then becomes:
then becomes:  A Z-score of 1.92 = .9726
The probability that a randomly selected bag contains between 1,000 and 1,500 chocolate chips:
A Z-score of 1.92 = .9726
The probability that a randomly selected bag contains between 1,000 and 1,500 chocolate chips: 
USING THE TI-83/84 CALCULATOR
Select: 2nd VARS → DISTR
CHOICE 2: normalcdf
normalcdf(1000,1500,1252,129)
Press: Enter
You should get:  , which is the probability that a randomly selected bag contains between 1,000 and 1,500 chocolate chips.
, which is the probability that a randomly selected bag contains between 1,000 and 1,500 chocolate chips.