Question 1097683: In a purse Misty has 1.91, including one more nickel than quarters. She also has twice as many dimes as nickels. But, she also has eight more pennies than dimes. How many of each of the four coins does Misty have?
****
So what I did was use the formula: Quantity X Value = Subtotal.
Found 5 solutions by richwmiller, josgarithmetic, ikleyn, greenestamps, MathTherapy:
Answer by richwmiller(17219)   (Show Source):
Answer by josgarithmetic(39617)  (Show Source):
Answer by ikleyn(52781)  (Show Source):
You can put this solution on YOUR website! .
In a purse Misty has 1.91, including one more nickel than quarters. She also has twice as many dimes as nickels.
But, she also has eight more pennies than dimes. How many of each of the four coins does Misty have?
~~~~~~~~~~~~~~~~~~~~~
Let N be the number of nickels.
Then the number of quarters is (N-1), according to the condition.
Also, the number of dimes is 2N.
In addition, the number of pennies is (2N+8).
Now we are ready to write the "money equation"
pennies + nickels + dimes + quarters = 191 cents, or
(2N+8) + 5N + 10*(2N) + 25*(N-1) = 191 cents.
Simplify and solve for N:
2N + 8 + 5N + 20N + 25N - 25 = 191 ====>
52N = 191 - 8 + 25 = 208 ====> N = 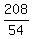 = 4.
Answer. 4 nickels, 3 quarters, 8 dimes and 16 pennies.
Check. 4*5 + 3*25 + 8*10 + 16 = 191 cent. ! Correct !
Solved.
----------------
For coin problems and their detailed solutions see the lessons in this site:
- Coin problems
- More Coin problems
- Solving coin problems without using equations
- Kevin and Randy Muise have a jar containing coins
- Typical coin problems from the archive
- Solving coin problems mentally by grouping without using equations
- Santa Claus helps solving coin problem
You will find there the lessons for all levels - from introductory to advanced,
and for all methods used - from one equation to two equations and even without equations.
Read them attentively and become an expert in this field.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Coin problems".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
Solving problems like this with formal algebra is of course good exercise in learning algebra. However, thinking through a problem with logical analysis can be an even better exercise for your brain. So let's think through this problem using the clues we have to find the answer. Then we can look at a formal algebraic solution.
The total value is $1.91, made up of pennies, nickels, dimes, and quarters. Since pennies are the only coins with values that are not multiples of 5, the number of pennies has to be one of these:
1, 6, 11, 16, 21, 26, ... etc.
But the number of pennies is 8 more than the number of dimes, so the number of pennies can't be 1 or 6.
So let's guess that the number of pennies is 11, and see what happens.
The number of pennies is 11, so the number of dimes is 3. The number of dimes is twice the number of nickels,....
Oops! This isn't going to work; the number of dimes has to be an even number.
So next let's see what happens if we guess the number of pennies is 16.
The number of pennies is 16, so the number of dimes is 8; then the number of nickels is 4. And using some information we haven't yet had a chance to use, the number of quarters is then 3.
So we have a potential answer of 3 quarters, 8 dimes, 4 nickels, and 16 pennies.
Does that give us the right total? Let's check.
3(25) + 8(10) + 4(5) + 16(1) = 75+80+20+16 = 191
Hooray! We found the answer.
Now for a solution using formal algebra.
You want to look for a way to define your variable(s) so that the work you have to do is as easy as possible. In particular, it is generally a good idea to avoid fractions if possible. In this problem, a bit of analysis shows that using either the number of quarters or the number of nickels is best. Then since the number of nickels is 1 more than the number of quarters, let's choose the number of quarters for our variable.
let x = number of quarters
then x+1 = number of nickels [one more than the number of quarters]
then 2x+2 = number of dimes [twice the number of nickels]
then 2x+10 = number of pennies [8 more than the number of dimes]
Now use your formula with these expressions and the values of each coin:
value of the quarters: 
value of the nickels: 
value of the dimes: 
value of the pennies: 
Then the total value of all the coins is
Now go back and substitute this value into the expressions for the numbers of the different coins; you get the answer:
3 quarters, 4 nickels, 8 dimes, 16 pennies
Answer by MathTherapy(10552)  (Show Source):
You can put this solution on YOUR website!
In a purse Misty has 1.91, including one more nickel than quarters. She also has twice as many dimes as nickels. But, she also has eight more pennies than dimes. How many of each of the four coins does Misty have?
****
So what I did was use the formula: Quantity X Value = Subtotal.
Only ONE VARIABLE is needed, and that's Q for the number of quarters
Then number of nickels = Q + 1
Number of dimes: 2(Q + 1), or 2Q + 2
Number of pennies: 2Q + 2 + 8, or 2Q + 10
We then get: .25Q + .05(Q + 1) + .1(2Q + 2) + .01(2Q + 10) = 1.91
.25Q + .05Q + .05 + .2Q + .2 + .02Q + .1 = 1.91
.25Q + .05Q + .2Q + .02Q + .05 + .2 + .1 = 1.91
.52Q + .35 = 1.91
.52Q = 1.56
|
|
|
