Question 1082146: A diplomat travels from point X to Y. If he will be departing X at 8:00 AM, and travel 2 kilometers per hour, he will arrive at Y, 3 minutes earlier than his expected time of arrival. However if he will leave at 8:30 AM and travel 2 3 kilometers per hour, he will arrive 6 minutes later than the expected time. What is the expected time of his arrival?
Answer by ikleyn(52775)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A diplomat travels from point X to Y. If he will be departing X at 8:00 AM, and travel 2 kilometers per hour,
he will arrive at Y, 3 minutes earlier than his expected time of arrival.
However if he will leave at 8:30 AM and travel  3 kilometers per hour, 3 kilometers per hour,
he will arrive 6 minutes later than the expected time. What is the expected time of his arrival?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let D be the unknown distance from X to Y.
Moving at 2 km/h, the diplomat will spend 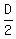 hours.
Moving at 3 km/h, the diplomat will spend hours.
Moving at 3 km/h, the diplomat will spend  hours.
The condition says hours.
The condition says
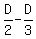 = 30 minutes + (6-3) minutes = 33 minutes. (It is the "time difference" equation)
Try to understand on your own how these numbers come from the condition
and how and why do they combine in this expression (30 + (6-3)) minutes.
But we need to write both sides of the last equation in uniform units. So, this equation will take the form = 30 minutes + (6-3) minutes = 33 minutes. (It is the "time difference" equation)
Try to understand on your own how these numbers come from the condition
and how and why do they combine in this expression (30 + (6-3)) minutes.
But we need to write both sides of the last equation in uniform units. So, this equation will take the form
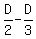 = = 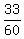 of an hour.
To solve this equation, multiply both sides by 60. You will get
30D - 20D = 33 ----> 10D = 33 ----> D = of an hour.
To solve this equation, multiply both sides by 60. You will get
30D - 20D = 33 ----> 10D = 33 ----> D = 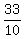 = 3.3 kilometers.
Thus we found the distance. It is 3.3 kilometers.
Now, at the second scenario, the diplomat starts at 8:30 am, moves = 3.3 kilometers.
Thus we found the distance. It is 3.3 kilometers.
Now, at the second scenario, the diplomat starts at 8:30 am, moves 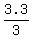 = 1.1 hour = 1 hour 6 minutes and arrives at 9:36 am,
which is 6 minutes late.
Hence, the meeting is scheduled at 9:30 am. = 1.1 hour = 1 hour 6 minutes and arrives at 9:36 am,
which is 6 minutes late.
Hence, the meeting is scheduled at 9:30 am.
Solved.
If you want to see another solved problems of this kind, look into the lesson
- How far do you live from school?
in this site.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this textbook under the section "Word problems", the topic "Travel and Distance problems".
|
|
|