Question 1068609: A paddle boat can move at a speed of 8 km/h in still water. The boat is paddled 4 km downstream in a river in the same time it takes to go 2 km upstream. What is the speed of the river?
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39616)   (Show Source): (Show Source):
Answer by ikleyn(52776)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A paddle boat can move at a speed of 8 km/h in still water. The boat is paddled 4 km downstream in a river in the same time
it takes to go 2 km upstream. What is the speed of the river?
~~~~~~~~~~~~~~~~~~~~~~
Let "v" be the speed of the river (or, better to say, current rate), in km/h.
Then the speed of the boat downstream is (8+v) km/h (relative to the river banks),
and the speed of the boat downstream is (8-v) km/h.
Therefore, the time for traveling 4 km downstream is 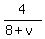 hours,
and the time for traveling 2 km upstream is hours,
and the time for traveling 2 km upstream is 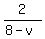 hours.
According to the condition, time hours.
According to the condition, time 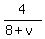 is the same as time is the same as time 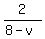 , which gives you an equation , which gives you an equation
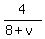 = = 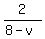 . (1)
It is your equation to find the unknown "v". To solve it, multiply both sides of (1) by (8+v)*(8-v). You will get
4*(8-v) = 2*(8+v).
Simplify and solve for v:
32 - 4v = 16 + 2v ---> 32 - 16 = 2v + 4v ---> 6v = 16 ---> v = . (1)
It is your equation to find the unknown "v". To solve it, multiply both sides of (1) by (8+v)*(8-v). You will get
4*(8-v) = 2*(8+v).
Simplify and solve for v:
32 - 4v = 16 + 2v ---> 32 - 16 = 2v + 4v ---> 6v = 16 ---> v = 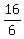 = =  km/h.
Answer. The current rate is km/h.
Answer. The current rate is  km/h = km/h =   km/h.
Check. Speed downstream is km/h.
Check. Speed downstream is 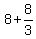 = = 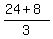 = = 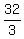 km/h; Time downstream is km/h; Time downstream is 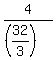 = =  = = 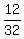 = =  of an hour.
Speed upstream is of an hour.
Speed upstream is 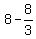 = =  = = 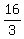 km/h; Time upstream is km/h; Time upstream is  = =  = =  = =  of an hour. of an hour.
Solved and checked.
It is a typical and standard Upstream and Downstream trip word problem.
You can find many similar fully solved problems on upstream and downstream trips with detailed solutions in lessons
- Wind and Current problems
- More problems on upstream and downstream round trips
- Selected problems from the archive on the boat floating Upstream and Downstream
in this site.
Read them attentively and learn how to solve this type of problems once and for all.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this textbook under the section "Word problems", the topic "Travel and Distance problems".
|
|
|