Question 1065741: The height of an object thrown upward with an initial velocity of 96 feet per second is given by the formula h=16t^2+96t, where t is the time in seconds
How long will it take the object to reach a height of 144 feet?
How long will it take the object to return to the point of departure?
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! There is a missing minus sign.
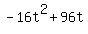   is the height (in feet) of the object  seconds after it is thrown up.
A graph of as a function of looks like this
When  , we have
 .
Solving that equation for we can find
when the object will reach a height of 144 feet
(as , in seconds after being thrown).
Dividing both sides of the equal sign by  ,
we get the equivalent equation
That can be solved by "completing the square":
So, the only solution is  .
The object is at a height of 144 ft only once,
 after being thrown up.
That means that it takes the object to reach a height of 144 feet.
It also means that  is the maximum height.
After 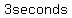 the object is falling back down.
Quadratic functions, like ,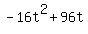
are symmetrical,
so if it takes the object  seconds to go
from  at  to ,
it will take another for the object to return
from to .
That is also obvious from the equation.
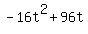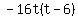
is zero obviously for and  .
So after reaching a maximum height of 144 feet at 3 seconds,
it takes the object  seconds
to come back down to the ground (to ).
|
|
|
