Question 106361: help!!! my # is a multiple of 150 -- 9 is a factor of my # -- my # has 3 digits
the sum of the # in my digit is 9
Answer by HyperBrain(694)   (Show Source): (Show Source):
You can put this solution on YOUR website! It is true that you number is divisible by 9 because the sum of its digits is 9 and a number is divisible by 9 if the sum of the digits is divisible by 9 (9 is divisible by 9)
It is a multiple of 150. And,  this means that it MUST end with a ZERO. this means that it MUST end with a ZERO.
Aso,  ---it is divisible by 50! that means it is just ending up with 00 or 50. ---it is divisible by 50! that means it is just ending up with 00 or 50.
AGAIN, the sum of the digits must be divisible by 9. Now, we know two things the second digit and the last digit---the second digit maybe a FIVE or a ZERO and the last didit is sure to be ZERO.
The sum maybe
1st digit+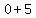 =1st digit + =1st digit +
or
1st digit +  = 1st digit = 1st digit
In the first case, there is one solution---450 (a multiple of 150, ends with 50, the sum is  which is divisible by 9. which is divisible by 9.
In the second case, there is also one solution---90( amultiple of 150, ends with 00, and the sum of the digits is  which is divisible by 9. which is divisible by 9.
Therefore, your number maybe 450 or 900.
Power up,
HyperBrain!
|
|
|