SOLUTION: A boat moves 7 kilometers upstream in the same amount of time it moves 20 kilometers downstream. If the rate of the current is 5 kilometers per hour, find the rate of the boat

Algebra ->  Customizable Word Problem Solvers  -> Misc -> SOLUTION: A boat moves 7 kilometers upstream in the same amount of time it moves 20 kilometers downstream. If the rate of the current is 5 kilometers per hour, find the rate of the boat      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 1059114: A boat moves 7 kilometers upstream
in the same amount of time it moves 20
kilometers downstream. If the rate of the
current is 5 kilometers per hour, find the
rate of the boat in still water.
Found 3 solutions by josgarithmetic, MathTherapy, ikleyn:
Answer by josgarithmetic(39616) About Me  (Show Source):
You can put this solution on YOUR website!
                 SPEED       TIME      DISTANCE
UPSTREAM          r-5         t           7
DOWNSTREAM        r+5         t          20


The problem form is so common, I will generalize.
                 SPEED       TIME      DISTANCE
UPSTREAM          r-c         t           p
DOWNSTREAM        r+c         t           d

p is for distance uPstream and d is distance Downstream.

The unknown variables are r and t.

You can form an equation because t is the same number for both directions and according to the constant travel rates rule.

highlight%28p%2F%28r-c%29=d%2F%28r%2Bc%29%29
Solve for r.

Answer by MathTherapy(10551) About Me  (Show Source):
You can put this solution on YOUR website!

A boat moves 7 kilometers upstream in the same amount of time it moves 20 kilometers downstream. If the rate of the current is 5 kilometers per hour, find the rate of the boat in still water.
Let boat's rate be S

Average speed:  

Time boat takes to travel 7 miles upstream = 7%2F%28S+-+5%29

Time boat takes to travel 20 miles downstream = 20%2F%28S+%2B+5%29

We then get the following TIME equation: 7%2F%28S+-+5%29+=+20%2F%28S+%2B+5%29

20(S - 5) = 7(S + 5) ------ Cross-multiplying

20S - 100 = 7S + 35

20S - 7S = 35 + 100

13S = 135

S, or speed of boat in still water = highlight_green%28matrix%281%2C4%2C+135%2F13%2C+or%2C+10%265%2F13%2C+%22km%2Fh%22%29%29

Answer by ikleyn(52775) About Me  (Show Source):
You can put this solution on YOUR website!
.
A boat moves 7 kilometers upstream in the same amount of time it moves 20 kilometers downstream.
If the rate of the current is 5 kilometers per hour, find the rate of the boat in still water.
~~~~~~~~~~~~~~~~~~~~~~~~~~~ 

Let "u" be the rate of the boat in still water, in km%2Fh.

Then your governing equation ("time equation") is

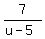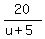7%2F%28u-5%29 = 20%2F%28u%2B5%29.

The left side is the time to travel 7 kilometers upstream.

The right side is the time to travel 20 kilometers downstream.

To solve the equation, multiply both sides by (u-5)*(u+5). You will get


7(u+5) = 20(u-5),  or

7u + 35 = 20u - 100,  or

35 + 100 = 20u - 7u,  or

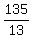135 = 13u  --->  u = 135%2F13.


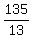Answer. The rate of the boat in still water is  135%2F13 km%2Fh.

        Unfortunately, the person who invented these input numbers, select them too curve to get an integer number as the answer.
        Perhaps, this person didn't solve the problem himself.

It is a typical "upstream and downstream Travel and Distance" word problem.

See the lessons
    - Wind and Current problems
    - More problems on upstream and downstream round trips
    - Selected problems from the archive on the boat floating Upstream and Downstream
in this site.

You will find the detailed solutions of many similar problems there.

Also, you have this free of charge online textbook in ALGEBRA-I in this site
    - ALGEBRA-I - YOUR ONLINE TEXTBOOK.

The referred lessons are the part of this textbook under the section "Word problems", the topic "Travel and Distance problems".


If after reading my solution you still have a question "why the governing equation has this form ?",
then read the lessons above. They contain the detailed answer to this question.