SOLUTION: Two mixtures contain p% and q% respectively of a certain ingredient. Show x units of the first is combined with y units of the second so the resulting mixture is r% of the ingredi

Algebra ->  Customizable Word Problem Solvers  -> Misc -> SOLUTION: Two mixtures contain p% and q% respectively of a certain ingredient. Show x units of the first is combined with y units of the second so the resulting mixture is r% of the ingredi      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 1054315: Two mixtures contain p% and q% respectively of a certain ingredient. Show x units of the first is combined with y units of the second so the resulting mixture is r% of the ingredient.
Unsure how to proceed. Thanks again.
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39627) About Me  (Show Source):
You can put this solution on YOUR website!
The description is just like any other of its kind, but just using variables for all values and numbers. I really, really, REALLY suggest you study this, which is the same thing, but just using other variables:

LESSON: Mixture for both material quantities unknown for a known amount of finished mixtures, https://www.algebra.com/my/Mixtures%3A-All-in-Symbols.lesson?content_action=show_dev

Answer by ikleyn(52864) About Me  (Show Source):
You can put this solution on YOUR website!
.
Two mixtures contain p% and q% respectively of a certain ingredient. Show x units of the first is combined with y units
of the second so the resulting mixture is r% of the ingredient.
Unsure how to proceed. Thanks again.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 

The correct question should be:

     "how x units of the first is combined with y units 
      of the second so the resulting mixture is r% of the ingredient?"


In other words, you are asked to find the ratio of "x" to "y" that provides r% concentration of the mixture.

The "concentration" equation is

px + qy = r(x+y).   (1)

The values "p", "q" and "r" are given; the ratio x%2Fy is under the question.

Based on the equation (1), collect the terms with x on the left and the therms with y on the right:

px - rx = ry - qy,   or

(p-r)x = (r-q)y.

It gives you

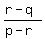x%2Fy = %28r-q%29%2F%28p-r%29.

Thus you found the ratio x%2Fy. 
The problem is solved.


By the way, the solution does exist if and only if  "r"  lies between the values of "p"  and  "q".

There is entire bunch of the lessons covering various types of mixture problems
    - Mixture problems
    - More Mixture problems
    - Solving typical word problems on mixtures for solutions
    - Word problems on mixtures for antifreeze solutions
    - Word problems on mixtures for dry substances like coffee beans, nuts, cashew and peanuts
    - Word problems on mixtures for dry substances like candies, dried fruits
    - Word problems on mixtures for dry substances like soil and sand
    - Word problems on mixtures for alloys
    - Typical word problems on mixtures from the archive
in this site.

Read them and become an expert in solution the mixture word problems.

Also, you have this free of charge online textbook in ALGEBRA-I in this site
    - ALGEBRA-I - YOUR ONLINE TEXTBOOK.

It contains many other solved word problems, as well as many other interesting and useful things.