Question 1036738: five baskets contain coconuts. the first and second baskets together have a total of 52 coconuts. the second and third baskets have 43 coconuts. the third and fourth baskets have 34 coconuts. the fourth and fifth baskets have 30 coconuts. and the first and fifth baskets have 47 coconuts. How many coconuts are in each basket?
Found 2 solutions by Edwin McCravy, ikleyn:
Answer by Edwin McCravy(20067)   (Show Source): (Show Source):
You can put this solution on YOUR website! five baskets contain coconuts. the first and second
baskets together have a total of 54 coconuts. the
second and third baskets have 38 coconuts. the third
and fourth baskets have 28 coconuts. the fourth and
fifth baskets have 25 coconuts. and the first and
fifth baskets have 49 coconuts. How many coconuts
are in each basket?
Notice that I have changed the number of coconuts in
the baskets. I did that so I wouldn't be doing your
work for you. You do your problem the exact same way.
Use this as a model:
Five baskets contain coconuts.
A = number of coconuts in the 1st basket.
B = number of coconuts in the 2nd basket.
C = number of coconuts in the 3rd basket.
D = number of coconuts in the 4th basket.
E = number of coconuts in the 5th basket.
the first and second baskets together have a total of 54 coconuts.
A + B = 54
the second and third baskets have 38 coconuts.
B + C = 38
the third and fourth baskets have 28 coconuts.
C + D = 28
the fourth and fifth baskets have 25 coconuts.
D + E = 25
and the first and fifth baskets have 49 coconuts.
A + E = 49
So the system of equations is:
(1) A + B = 54
(2) B + C = 38
(3) C + D = 28
(4) D + E = 25
(5) A + E = 49
Solve (5) for A: A = 49-E, substitute in (1)
49-E + B = 54. Solve for B: B = 5+E. Substitute in (2)
5+E + C = 38. Solve for C: C = 33-E. Substitute in (3)
33-E + D = 28. Solve for D: D = E-5. Substitute in (4)
E-5 + E = 25. Solve for E: 2E = 30, E = 15
Substitute E=15 in D = E-5 = 15-5 = 10
Substitute E=15 in C = 33-E = 33-15 = 18
Substitute E=15 in B = 5+E = 5+15 = 20
Substitute E=15 in A = 49-E = 49-15 = 34
Now use the above to solve your problem the exact same way.
Edwin
Answer by ikleyn(52945)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Five baskets contain coconuts. the first and second baskets together have a total of 52 coconuts.
The second and third baskets have 43 coconuts. The third and fourth baskets have 34 coconuts.
The fourth and fifth baskets have 30 coconuts, and the first and fifth baskets have 47 coconuts.
How many coconuts are in each basket?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let  be the number of coconuts in the i-th basket, i = 1, 2, 3, 4, 5.
Then we have this system of 5 equations in 5 unknowns: be the number of coconuts in the i-th basket, i = 1, 2, 3, 4, 5.
Then we have this system of 5 equations in 5 unknowns:
 + +  = 52, (1) = 52, (1)
 + +  = 43, (2) = 43, (2)
 + +  = 34, (3) = 34, (3)
 + + 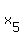 = 30, (4) = 30, (4)
 + + 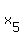 = 47. (5)
Add all 5 equations (1) to (5) (both sides). You will get = 47. (5)
Add all 5 equations (1) to (5) (both sides). You will get
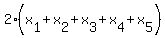 = 206, or, dividing both sides by 2 = 206, or, dividing both sides by 2
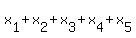 = 103. (6).
Now, add equations (2) and (4) and distract this sum from (6). You will get = 103. (6).
Now, add equations (2) and (4) and distract this sum from (6). You will get
 = 103 - 43 - 30 = 30.
So, there are 30 coconuts in basket #1.
Next, add equations (1) and (4) and distract this sum from (6). You will get = 103 - 43 - 30 = 30.
So, there are 30 coconuts in basket #1.
Next, add equations (1) and (4) and distract this sum from (6). You will get
 = 103 - 52 - 30 = 21.
So, there are 21 coconuts in basket #3.
Next, add equations (1) and (3) and distract this sum from (6). You will get = 103 - 52 - 30 = 21.
So, there are 21 coconuts in basket #3.
Next, add equations (1) and (3) and distract this sum from (6). You will get
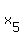 = 103 - 52 - 34 = 17.
So, there are 30 coconuts in basket #5.
Now, from (1) you have = 103 - 52 - 34 = 17.
So, there are 30 coconuts in basket #5.
Now, from (1) you have  = 52 - = 52 -  = 52 - 30 = 22 coconuts in basket #2.
And finally, from (4) you have = 52 - 30 = 22 coconuts in basket #2.
And finally, from (4) you have  = 30 - = 30 - 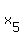 = 30 - 17 = 13 coconuts in basket #4.
Answer. 30, 22, 21, 13 and 17 coconuts in baskets 1 to 5 respectively. = 30 - 17 = 13 coconuts in basket #4.
Answer. 30, 22, 21, 13 and 17 coconuts in baskets 1 to 5 respectively.
|
|
|