Question 1030182: A right circular cone is inscribed inside a larger right circular cone with a volume of 150 cm3. The axes of the cones coincide and the vertex of the inner cones touches the center of the base of the outer cone. Find the ratio of the heights of the cones that maximizes the volume of the inner cone.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! By not giving enough data to find the radius of height, or height to radius ratio of the larger cone, the problem's wording hints that the answer does not depend on the height to radius ratio of the larger cone.
I do not believe you need to know the volume of the larger cone, either.
If there is a way to solve the problem without invoking calculus,
or if there is an easier or more elegant way to reach the answer,
let me know.
The way I saw to the solution is shown below.
Here is a cross-section of the cones, sliced along their axes.
 The cones heights are The cones heights are 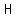 and and  ; their radii are ; their radii are  and and  . .
The portion of the large cone above the base of the small cone is
a cone similar to the large cone (same shape, but scaled down).
Therefore, their corresponding length measurements are proportional:
 <--> <-->  <-- <--  . .
The volume of the small cone is
 . .
Substituting 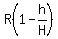 for for  , we get , we get




That is a function of  , with , with  and and 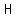 being constants. being constants.
The derivative is

The maxima and minima of  will happen when will happen when  , ,
and that will happen when  . .
If you change the name of the variables to  , you can re-write the equation as , you can re-write the equation as
 , and you would recognize it as a quadratic equation, , and you would recognize it as a quadratic equation,
with solutions  (meaning (meaning  ) )
and  (meaning (meaning  ). ).
The polynomial  , and , and 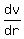 changes sign at each of its two zeros, changes sign at each of its two zeros,
so one must be a maximum and the other a minimum.
 makes makes  and and  , so for , so for  the small cone volume is minimum. the small cone volume is minimum.
The maximum volume for the small cone happens when  . .
|
|
|