SOLUTION: how many distinguishable permutations can be formed from the letters in the word success? -----This is the first time I am seeing a problem like this. I'm sure it is simple to u

1. Let us start from more simple case. Imagine that you have the word consisting of three identical letters, 
   for example, the word "ooo" of three "o".
   How many distinguishable permutations can you have with three "o"?
   Think one minute. But of course, only one. Nothing more.
   You can move these letters from place to place, but you can not get nothing new.

2. Next, imagine that you have the word "ogo".
   How many permutations can you have?
   Only three: "goo", "ogo" and "oog". Nothing more.
   The theory says that you can have 6 permutations of three objects.
   But it is only in the case when all three your objects are distinguishable (which is assumed by default).

3. OK. So, you see that there is a problem here.

4. Now consider the word "Ogo" of three letters, consisting of one capital "O", "g" and small (lover case) "o".
   Let us assume that we are able to make a distinguish between capital "O" and lover-case "o". (But of course, we can).
   How many permutations do we have of these three symbols? Here they are in two lines:
       gOo, Ogo, Oog,
       goO, ogO, oOg.

   Until we can distinguish "O" and "o", we have 6 permutations.
   But once we loss this ability, we have only three of them.

   Why? Simply because every two permutations (every two 3-letter words) that differ in the ordering the letters "O" and "o" 
   in the line (in the string) merge into ONE 3-letter word. They TWO simply become ONE 3-letter word. 
   TWO initially different permutations/words become ONE word.
   EVERY two initially different permutations that differ in the ordering "O" and "o" merge and become ONE permutation.

5. This analysis works for any n-letter word that contains two identical letters and (n-2) different remaining letters.

   Therefore, instead of n! permutations of n distinguished objects you will have only half of them 
   in the case when TWO objects are identical (undistinguished). The half is .

6. If you followed me to this point, you can easily continue on your own and consider the case when your n-letter word 
   contains TWO different pairs of undistinguished letters.

   How many permutations will you have in this case?

   .

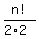7. Now apply it to the word "success".


   Ooo! It contains THREE "s" and TWO "c".

   So, you need to make one more step further.

   My answer is  .

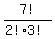   2!  goes for two "c" and  3!  goes for three "s".


   And yours ??