Question 1023225: It takes Earth approximately 365.2422 days to orbit the sun once, this is known as the tropical year and is the length of the cycle of seasons. In a regular year, there are 365 days, and in a leap year there are 366 days. In a four-year period, one year being a leap year, what is the absolute difference between the number of days observed in the calendar years and the number of days in four tropical years? Express your answer as a decimal to the nearest ten-thousandth.
Thank you and please show all work to get you to the solution. Thanks
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The number of days in a period of four consecutive calendar years where one year is a leap year is the integer number
 , ,
which we can express as 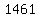 to the nearest ten-thousandth, to the nearest ten-thousandth,
because  is one ten-thousandth. is one ten-thousandth.
The number of days in four orbits of Earth is the non-integer number
 . .
The difference is
 . .
NOTES:
1) The length of the tropical year changes a little over the centuries, but for now  is a good approximation. is a good approximation.
(I did not know that before your question, so thank you for the learning opportunity).
Since  is a good approximation, is a good approximation,
we do not have to worry about 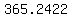 , given with 4 decimal places, , given with 4 decimal places,
not being precise enough to make 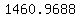 not being not being 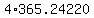 to the nearest to the nearest  . .
2) Calendar years are leap years if divisible by  , but not by , but not by  unless divisible by unless divisible by  , ,
so in  years there are years there are  leap years, leap years,
and the average length of a calendar year is  . .
(I was taught that in the 9th grade, and it stuck with me).
|
|
|