Question 1009194: Problem 1
Let f(x) = (a – 5)x^2 + (b – 3)x + c and g(x) = 3x^2 – 5x – 4.
If f(1) = g(1), f(-8) = g(-8), f(-79) = g(-79), find the value of a + 2b + 2c.
Problem 2
A video production company is planning to produce an instructional movie. The producer estimates that it will cost $250,000 to shoot the video and $150 per unit to copy and distribute the CD. The wholesale price of the disc is $750 per unit.
a. Write the cost function C, the revenue function R, and the profit function P.
b. How many CD units must be sold in order to have a profit? A loss? A break-even?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! first proglem:
unless i'm missing something, i believe f(x) will be equal to g(x) when (a-5) = 3 and (b-3) = -2 and c = -4
when that happens, f(x) and g(x) will be identical.
a-5 = 3 when a = 8
b - 3 = -5 when b = -2
c = -4 when c = -4
you get a = 8, b = -2, c = -4
a + 2b + 2c is therefore equal to 8 + (-4) + (-8) which is equal to 8 - 12 which is equal to -4.
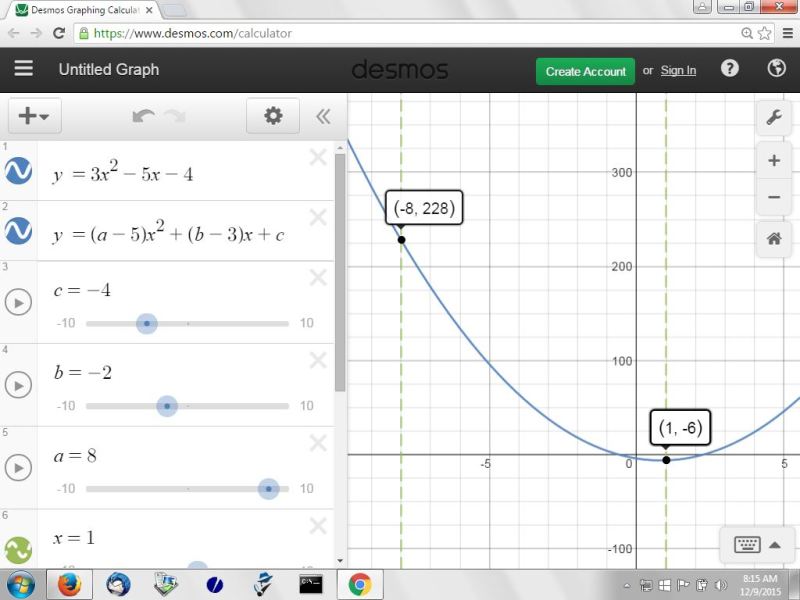
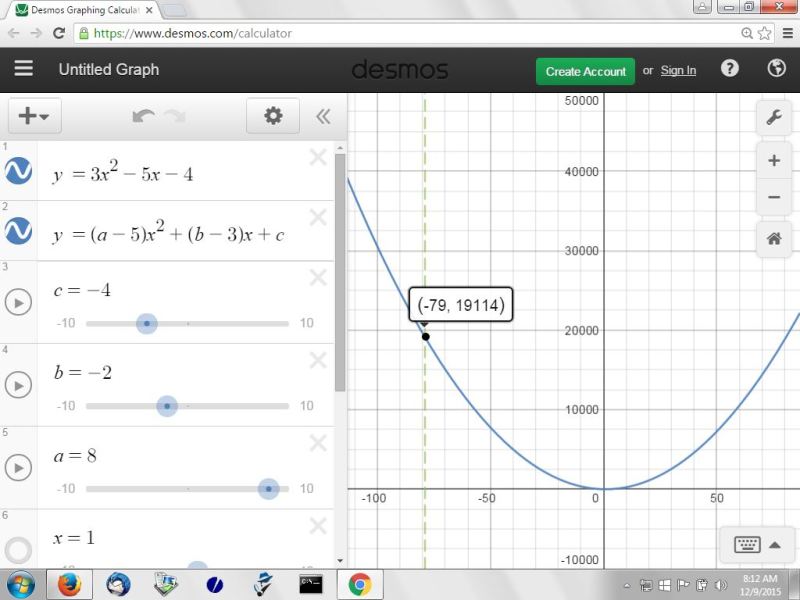
here's the graph of both equations.
this graph shows that the values of:
f(1) and g(1) are the same
f(-8) and g(-8) are the same.
f(-79) and g(-79) are the same.
first graph shows f(1) and f(-8) which are the same as g(1) and g(-8).
second graph shows f(-79) which is the same as g(-79).
second problem:
A video production company is planning to produce an instructional movie. The producer estimates that it will cost $250,000 to shoot the video and $150 per unit to copy and distribute the CD. The wholesale price of the disc is $750 per unit.
a. Write the cost function C, the revenue function R, and the profit function P.
b. How many CD units must be sold in order to have a profit? A loss? A break-even?
cost function is c = 250,000 + 150 * x
x = number of units.
revenue function is r = 750 * x
profit function is p = r - c
r is the revenue
p is the profit
x is the number of units produced and sold.
c is the cost.
break even is when the revenue equal the cost.
you will get r = c which then becomes:
750 * x = 250,000 + 150 * x
subtract 150 * x from both sides of this equation to get:
750 * x - 150 * x = 250,000
combine like terms to get:
600 * x = 250,000
solve for x to get:
x = 250,000 / 600 = 416 and 2/3 units.
he will break even when he produces and sells 416 and 2/3 units.
if he produces and sells less than that, he will lose money.
if he produces and sells more than that, he will make money.
examples:
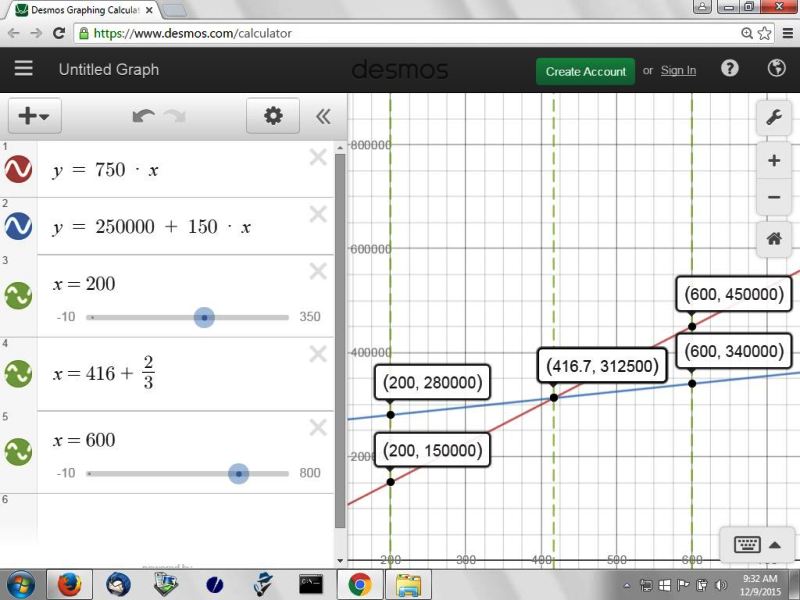
he produces and sells 416 and 2/3 units.
revenue is 750 * 416 and 2/3 = 312,500.
cost is 250,000 + 150 * 416 and 2/3 = 312,500.
he broke even.
he produces and sells 200 units.
revenue is 750 * 200 = 150,000
cost is 250,000 + 150 * 200 = 280,000
he loses money.
he produces and sells 600 units.
revenue is 750 * 600 = 450,000
cost is 250,000 + 150 * 600 = 340,000
he makes money.
this is shown graphically below:
the blue line represents the cost.
the red line represents the revenue.
in formula terms:
break-even is when r = c
profit is when r > c
loss is when r < c
this leads to the following equations:
750*x = 250,000 + 150*x (break-even)
750*x > 250,000 + 150*x (make a profit)
750*x <= 250,000 + 150*x (take a loss)
i specifically said "produces and sells".
this is an important assumption.
it is possible that he can produce more than he sells.
that becomes a different type of problem that is more complex to solve.
i'm assuming you are not into those types of problems yet.
hence the assumption.
|
|
|