Question 100139: A club charters a plane at a cost of $15840 to take a group of members on a trip. At the last minute, 6 people in the group canceled, increasing the cost per person by $20. How many people originally intended to take this trip?
I set the original # of people = P
Cost/person = 15840/P
The people that went were = (P-6)
Final cost/person = 15840/(P-6)= 15840/P + 20
I did do a methodical 'guess and check' and did get what I think is the right answer (72), but how do I really work it out. On a test, that will be too time
consuming and in the real work, it is not practical.
Help! Also what would you classify this problem as?
Thanks
Found 2 solutions by stanbon, bucky:
Answer by stanbon(75887)   (Show Source):
You can put this solution on YOUR website! 15840/(P-6)= 15840/P + 20
Multiply thru by P(P-6) to get:
15840P = 15840(P-6) + 20P(P-6)
15840P -15840P +15840*6 = 20P^2-120P
20P^2-120P-15840*6 = 0
Divide thru by 20 to get:
P^2 - 6P -792*6 = 0
(P - 72)(P + 66) = 0
Positive answer:
P = 72
=================
Cheers,
Stan H.
Answer by bucky(2189) (Show Source):
You can put this solution on YOUR website! I set the original # of people = P <==== OK
.
Cost/person = 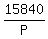 <==== This is the original cost per person and is OK
.
The people that went were = (P-6) <==== actual number of people that went
.
The cost/person for those that actually went = 
.
The cost/person for the people that actually went was $20 more/person than if all the original
persons had gone. Therefore, you can write this difference as:
.
 <=== this is just a different way of writing the equation you got.
.
A common denominator of the terms on the left side is  . To get the common
denominator for each term on the left side, multiply the first term by  and the second
term by 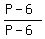 . Note that since these two multipliers have their numerators equal
to their denominators, we are actually multiplying each term by an equivalent of 1, so we
are not changing the equation at all. Doing the multiplication:
.
.
Doing the multiplication results in:
.
.
Do the distributed multiplication of the numerator of the second term:
.
.
The -15840*6 multiplies out to -95040 and the equation becomes:
.
.
Because the two terms on the left have the same denominator, you can combine their numerators
over the common denominator:
.
.
If you remove the parentheses in the numerator, it becomes:
.
.
And the two terms in the numerator that contain P are equal and opposite signs. Therefore, they
cancel and the equation reduces to:
.
.
Get rid of the denominator on the left side by multiplying both sides by  and
the equation becomes:
.
.
Multiply out the right side and the equation is then:
.
.
Subtract 95040 from both sides to get:
.
.
Transpose both sides to put the equation into a more standard form of:
.
.
All the terms have 20 as a common factor. Therefore, you can divide each term on both sides
by 20 to get:
.
.
This is a quadratic equation. If you are inordinately perceptive you might see that this
factors to:
.
.
And you could solve for P by setting each of the two factors equal to zero to get that
the two solutions to the equation are either P = +72 or P = -66. Obviously, minus 66 people
did not go and therefore, +72 people were originally to go.
.
However, it's not likely to see that factoring. Therefore, you can use the quadratic formula
to solve the equation:
.
.
Note that this quadratic equation is in the form of:
.
.
in which x = P, a = 1, b = -6, and c = -4752
.
The quadratic formula says that for an equation of the form will have
as its solutions the values:
.
.
Substitute the corresponding values above for x, a, b, and c to get:
.
.
Inside the radical ... (-6)^2 = 36 and -4*1*(-4752) = 19008. Substitute these to get:
.
.
Combine the terms under the radical and you get:
.
.
Take the square root of 19044 with your calculator and you get 138 ... which makes the
equation become:
.
.
The denominator multiplies out to 2 and in the numerator the -(-6) becomes +6. So the equation
reduces to:
.
.
This makes the two answers:
.
 which reduces to 
.
and
.
 which reduces to 
.
Again, -66 cannot be the answer. So the only answer that will work is +72 as the number of
people that were to go originally.
.
And also again, the equation you have to solve is classified as a quadratic equation.
.
Hope this helps you to see a way of doing the problem other than a "guess and check" method.
.
|
|
|
