This Lesson (In a jar, all but 6 are red marbles) was created by by ikleyn(52781)   : View Source, ShowAbout ikleyn:
In a jar, all but 6 are red marbles
Problem 1In a jar of red, green, and blue marbles, all but 6 are red marbles, all but 8 are green, and all but 4 are blue.
What percent of the marbles aren’t blue ?
Solution
From the condition, we can determine how many marbles of each color were there in the jar.
Indeed, we have these equations, where R is the number of red marbles, G is the number of green marbles and B is the number of blue marbles
G + B = 6 (1) ("all but 6 are red marbles")
R + B = 8 (2) ("all but 8 are green marbles")
R + G = 4 (3) ("all but 4 are blue marbles")
------------------------ Add equations (1), (2) and (3)
2*(R + G + B) = 6 + 8 + 4 = 18 ===========>
R + G + B = 9. (4)
Now, subtracting from equation (4) equations (1), (2) and (3), one after another separately, we get
R = 3; G = 1; B = 5.
Now the answer to the problem's question is
The ratio is 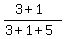 = =  ;
The percentage is ;
The percentage is 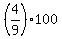 = 44.44%. ANSWER = 44.44%. ANSWER
My other additional lessons on Miscellaneous word problems in this site are
- I do not have enough savings now
- How many boys and how many girls are there in a family ?
- What is the last digit of the number a^n ?
- Find the last three digits of these numbers
- What are the last two digits of the number 3^123 + 7^123 + 9^123 ?
- Advanced logical problems
- Prove that if a, b, and c are the sides of a triangle, then so are sqrt(a), sqrt(b) and sqrt(c)
- Calculus optimization problems for shapes in 2D plane
- Calculus optimization problems for 3D shapes
- Solving some linear minimax problems in 3D space
- Solving one non-linear minimax problems in 3D space
- Solving linear minimax problem in three unknowns by the simplex method
- The "pigeonhole principle" problems
- In the worst case
- Page numbers on the left and right facing pages of an opened book
- Selected problems on counting elements in subsets of a given finite set
- How many integer numbers in the range 1-300 are divisible by at least one of the integers 4, 6 and 15 ?
- Nice problems to setup them using Venn diagram
- Wrapping a gift
- In preparation for Halloween
- Nice entertainment problems related to divisibility property
- Stars and bars method for Combinatorics problems
- Math Olympiad level problem on caves and bats
- Math Olympiad level problem on caught fishes
- Math Olympiad level problem on pigeonhole principle
- Math Olympiad level problem on placing books in bookcase
- OVERVIEW of additional lessons on Miscellaneous word problems
Use this file/link ALGEBRA-I - YOUR ONLINE TEXTBOOK to navigate over all topics and lessons of the online textbook ALGEBRA-I.
Use this file/link ALGEBRA-II - YOUR ONLINE TEXTBOOK to navigate over all topics and lessons of the online textbook ALGEBRA-II.
This lesson has been accessed 1836 times.
|