Lesson How many lollipops do the children have?

This Lesson (How many lollipops do the children have?) was created by by ikleyn(52781)

: View Source, Show
About ikleyn:

How many lollipops do the children have?

Problem 1

Joe, Amirah, Gastle and Sharifa had some lollipops. Joe had 5 lollipops less than 1/3 the total number of lollipops.
Amirah had 36 lollipops more than 1/3 the total number of lollipops. Gastle had 1/5 the number of lollipops Joe had
and Sharifa had 5 lollipops less than Gastle. How many lollipops were there in total?

Solution

Let x be one third of the total number of lollipops.

Then Joe had x - 5 lollipops.

Then Amirah had x + 36 lollipops.

Gastle had 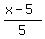 lollipops.

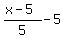Sharifa had  lollipops.

The equation is:

Joe + Amira + Gastle + Sharifa = 3x,   or

(x-5) + (x+36) + 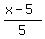 +  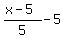= 3x.

Multiply both sides by 5. You will get

5x - 25 + 5x + 180 + x-5 + x-5 - 25 = 15x,   or

12x + 120 = 15x,

3x = 120. 

It is exactly what the problem is asking for.


Answer.  120 lollipops.

The lesson to learn from this solution is: a good choice of an unknown variable can save your effort and make the solution easier.

My other lessons on Miscellaneous word problems in this site are

    - Some logic problems
    - How to algebreze and to solve word problems on numbers?
    - Problem on two-wheel and three-wheel bicycles
    - Problem on animals at a farm
    - Problem on pills in containers
    - What type of problems are these?
    - Virtual exchange between two persons
    - Word problems on reversing digits of numbers
    - Spending money according to dates
    - Counting elements in sub-sets of a given finite set
    - How many subsets are there in a given finite set of n elements?
    - In how many ways the number 27720 can be split into a product of two co-prime factors?
    - Advanced problems on counting elements in sub-sets of a given finite set
    - Challenging problems on counting elements in subsets of a given finite set
    - Had they sold . . .
    - HOW TO algebreze and solve these problems?

    - How many coconuts are there in each of five baskets?
    - Tom the cat is brushing up his Math skills
    - Three grasshoppers play leapfrog along a line
    - The gardener's problem on a miracle tree in an enchanted garden
    - Water level rise in a tank after submerging bodies
    - Burning candles
    - Gaining clock problem
    - Finding the value of infinite continued fraction
    - Three circles touching externally
    - Solving minimax problems by the Linear Programming method
    - One unusual mimimax problem on joint work
    - Classic entertainment problems
    - More complicated but still elementary logic problems
    - Miscellaneous word problems for the day of April, 1
    - OVERVIEW of lessons on Miscellaneous word problems.

Use this file/link ALGEBRA-I - YOUR ONLINE TEXTBOOK to navigate over all topics and lessons of the online textbook ALGEBRA-I.

This lesson has been accessed 1660 times.