This Lesson (How many coconuts are there in each of five baskets?) was created by by ikleyn(52781)   : View Source, ShowAbout ikleyn:
How many coconuts are there in each of five baskets?
Problem 1Five baskets contain coconuts. The first and second baskets together have a total of 52 coconuts.
The second and third baskets have 43 coconuts. The third and fourth baskets have 34 coconuts.
The fourth and fifth baskets have 30 coconuts, and the first and fifth baskets have 47 coconuts.
How many coconuts are in each basket?
Solution
Let  be the number of coconuts in the i-th basket, i = 1, 2, 3, 4, 5.
Then we have this system of 5 equations in 5 unknowns: be the number of coconuts in the i-th basket, i = 1, 2, 3, 4, 5.
Then we have this system of 5 equations in 5 unknowns:
 + +  = 52, (1) = 52, (1)
 + +  = 43, (2) = 43, (2)
 + +  = 34, (3) = 34, (3)
 + + 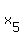 = 30, (4) = 30, (4)
 + + 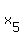 = 47. (5)
Add all 5 equations (1) to (5) (both sides). You will get = 47. (5)
Add all 5 equations (1) to (5) (both sides). You will get
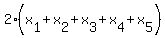 = 206, or, dividing both sides by 2 = 206, or, dividing both sides by 2
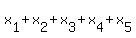 = 103. (6).
Now, add equations (1) and (4) and distract this sum from (6). You will get = 103. (6).
Now, add equations (1) and (4) and distract this sum from (6). You will get
 = 103 - 52 - 30 = 21.
So, there are 21 coconuts in basket #3.
Next, from equation (2) you can easily get get = 103 - 52 - 30 = 21.
So, there are 21 coconuts in basket #3.
Next, from equation (2) you can easily get get
 = 43 - = 43 -  = 43 - 21 = 22.
So, there are 22 coconuts in basket #2.
Then from equation (1) you can easily get = 43 - 21 = 22.
So, there are 22 coconuts in basket #2.
Then from equation (1) you can easily get
 = 52 - = 52 -  = 52 - 22 = 30.
So, there are 30 coconuts in basket #1.
Similarly, from equation (3) you can easily get = 52 - 22 = 30.
So, there are 30 coconuts in basket #1.
Similarly, from equation (3) you can easily get
 = 34 - = 34 -  = 34 - 21 = 13.
So, there are 13 coconuts in basket #4.
Then from (4) you have = 34 - 21 = 13.
So, there are 13 coconuts in basket #4.
Then from (4) you have 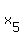 = 30 - = 30 -  = 30 - 13 = 17 coconuts in basket #5.
Answer. 30, 22, 21, 13 and 17 coconuts in baskets 1 to 5 respectively. = 30 - 13 = 17 coconuts in basket #5.
Answer. 30, 22, 21, 13 and 17 coconuts in baskets 1 to 5 respectively.
My other lessons on Miscellaneous word problems in this site are
Use this file/link ALGEBRA-I - YOUR ONLINE TEXTBOOK to navigate over all topics and lessons of the online textbook ALGEBRA-I.
This lesson has been accessed 2691 times.
|

