This Lesson (HOW TO calculate the distance from a point to a straight line in a coordinate plane) was created by by ikleyn(52781)   : View Source, ShowAbout ikleyn:
HOW TO calculate the distance from a point to a straight line in a coordinate plane
Let assume you are given a straight line in a coordinate plane by a linear equation
 (1) (1)
and the point P = P( , , ) by its coordinates (Figure 1). ) by its coordinates (Figure 1).
How to find the distance from a point to a straight line?
According to the lesson The distance from a point to a straight line
in a coordinate plane under the topic Introduction to vectors,
addition and scaling of the section Algebra-II in this site,
the distance from a point to a straight line is equal to
 = =  . (2) . (2)
|

Figure 1. The straight line  , ,
the point P( , , ) and the distance ) and the distance 
from the point P to the straight line
|
As it is explained in the lesson The distance from a point to a straight line in a coordinate plane, the distance from a point to a straight line is the length of the perpendicular drawn from the given point to the straight line. It is shown in red in the Figure 1. This perpendicular is the shortest segment among all the straight segments connecting the point with the straight line. The formula (2) expresses the length of this perpendicular. The examples below show how the formula (2) works.
Problem 1
Find the distance from the point P = (8,-1) to the straight line  (Figure 2). (Figure 2).
Solution
Use the formula (2) with a = 2, b = -1, c = -2,  = 8 and = 8 and  = -1. You have = -1. You have
 = = 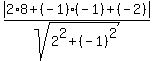 = = 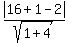 = = 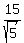 = =  . .
Answer. The distance is equal to  . .
|

Figure 2. The straight line  , ,
the point P( , , ) and the distance ) and the distance 
from the point P to the straight line
|
Problem 2
Find the distance from the point P = (-8,-1) to the straight line  (Figure 3). (Figure 3).
Solution
Use the formula (2) with a = 3, b = 2, c = 0,  = -8 and = -8 and  = -1. You have = -1. You have
 = = 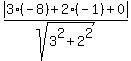 = = 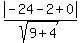 = =  = = 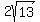 . .
Answer. The distance is equal to 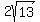 . .
|

Figure 3. The straight line  , ,
the point P( , , ) and the distance ) and the distance 
from the point P to the straight line
|
Problem 3
Find the distance from the point P = (2,5) to the straight line  (Figure 4). (Figure 4).
Solution
First, transform the equation of the given straight line to the canonical form (2).
It is  . .
Now use the formula (2) with a = 1, b = -2, c = -2,  = 2 and = 2 and  = 5. You have = 5. You have
 = =  = =  = = 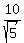 = =  . .
Answer. The distance is equal to  . .
|

Figure 4. The straight line  , ,
the point P( , , ) and the distance ) and the distance 
from the point P to the straight line
|
Problem 4
Find the distance from the point P = (6,3) to the straight line  (Figure 5). (Figure 5).
Solution
This time our straight line is the vertical line  . .
It seems as the singular case, but the procedure works smoothly for this case too.
Use the formula (2) with a = 1, b = 0, c = -2.5,  = 6 and = 6 and  = 3. You have = 3. You have
 = =  = = 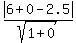 = = 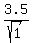 = =  . .
Taking into account that the straight line is vertical in this case, you
|

Figure 5. The straight line  and the point P( and the point P( , , ) )
|
could calculate the distance simply as the difference of x-coordinates  = = 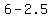 = =  . Surely, the result is the same. . Surely, the result is the same.
Answer. The distance is equal to  - -  = =  . .
Problem 5
Find the distance from the point P = (6,3) to the straight line  (Figure 6). (Figure 6).
Solution
This time our straight line is the horizontal line  . .
Use the formula (2) with a = 0, b = 1, c = 2.5,  = 6 and = 6 and  = 3. You have = 3. You have
 = = 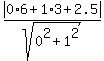 = = 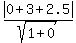 = = 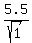 = = 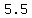 . .
Taking into account that the straight line is horizontal in this case, you
|

Figure 6. The straight line  and the point P( and the point P( , , ) )
|
could calculate the distance simply as the difference of y-coordinates  = = 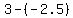 = = 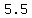 . Surely, the result is the same. . Surely, the result is the same.
Answer. The distance is equal to  - - 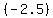 = = 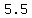 . .
Problem 6
Find the distance from the point P = (4,1) to the straight line  (Figure 7). (Figure 7).
Solution
Use the formula (2) with a = 1, b = -2, c = 1,  = 4 and = 4 and  = 1. You have = 1. You have
 = = 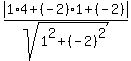 = = 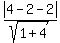 = = 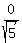 = =  . .
The found value of  is equal to zero. is equal to zero.
|

Figure 7. The straight line 
and the point P( , , ) )
|
Just the numerator of the expression for  is equal to zero, which means that the point P belongs to the straight line. is equal to zero, which means that the point P belongs to the straight line.
Answer. The distance is equal to  : the given point lies in the straight line. : the given point lies in the straight line.
Thus we checked that the formula (2) works in all cases.
The given point lies in the straight line if and only if the distance from the point to the line is equal to zero.
This is exactly the case when the numerator of the formula (2) has the zero value.
Other lessons on this topic in this site are
- The distance from a point to a straight line in a coordinate plane
- Using formula for the distance from a point to a straight line in a plane to solve word problems
- Two chords in a circle are congruent if and only if they are equally remoted from the center
- OVERVIEW of lessons on the distance from a point to a straight line in a coordinate plane
Use this file/link ALGEBRA-II - YOUR ONLINE TEXTBOOK to navigate over all topics and lessons of the online textbook ALGEBRA-II.
This lesson has been accessed 4647 times.
|

