Question 998202: Anne is standing on a straight road and wants to reach her helicopter which is located 2 miles down the road for her and a mile off the road in a field. she can run 5 miles an hour on the road and 3 miles per hour in the field. she plans to run down the road, then cut diagonally across the field to reach the helicopter.
where should she leave the road in order to reach the helicopter in exactly 42 minutes (0.7 hour)
where should she leave the road in order to reach the helicopter as soon as possible.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's say Anne runs at 5 mph down the road,
until she is  miles before the point directly in front of the helicopter. miles before the point directly in front of the helicopter.
Then, she runs across the field in a straight line towards the helicopter.
The road, field, helicopter, and Anne's path look like this: 
So Anne runs on the road for 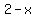 miles at miles at  mph in mph in 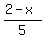 hours. hours.
Then, she runs across the field for 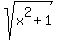 miles at miles at  mph in mph in 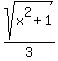 hours. hours.
Anne's total time as a function of  is is
 hours. hours.
If Anne wants to reach the helicopter in exactly 42 minutes (0.7 hour),  must be such that must be such that












The two solutions are:
 (rounded), meaning Anne runs (rounded), meaning Anne runs
 miles down the road, and then leaves the road, and miles down the road, and then leaves the road, and
 (rounded), meaning Anne runs (rounded), meaning Anne runs
 miles down the road, and then leaves the road. miles down the road, and then leaves the road.
If Anne wants to reach the helicopter as soon as possible, we must chose  to make to make 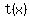 minimum. minimum.
I cannot think of another way other than resorting to calculus,
unless you are expected to use a graphing calculator (or a spreadsheet) to get an approximate answer.
The derivative of  is is


When 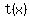 is minimum, is minimum,  , meaning that , meaning that
 --> --> --> --> --> --> --> --> --> --> --> --> --> -->
So, if Anne wants to reach the helicopter as soon as possible,
she should leave the road after running (((2-0.75=highlight(1.25)}}} miles.
|
|
|