Question 98653: Find the dimensions of a rectangle whose area is 180cm^2 and whose perimeter is 54 cm.
Answer by praseenakos@yahoo.com(507)   (Show Source): (Show Source):
You can put this solution on YOUR website! Question:
Find the dimensions of a rectangle whose area is 180cm^2 and whose perimeter is 54 cm.
Answer:
Given that,
 and and

Perimeter of rectangle is given by the formula, 2( length + width)
==> 2( length + width) = 54
==> ( length + width) = 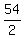
==> ( length + width) = 27
Now suppose, length = x cm
Then width = 27 - x
Now area is given by the formula, length * width
That is length * width = 180 cm^2
==> x * ( 27-x) = 180
==> 
==>  -----------------(1) -----------------(1)
This is a quadratic equation and you can solve this equation using quadratic formula for x.
==> 
Comparing equation(1) with the standard quadratic equation,
 , we have, , we have,
a = 1, b = -27 and c = 180
==> 
==> 
==> 
==> 
==> either,  or or 
==> either,  or or 
==> either,  or or 
that is either length = 15 cm of 12 cm
When length = 15 cm, width = 27 - 15 = 12 cm
And when length = 12cm, width = 27 - 12 = 15 cm.
Hence the solution.
Hope you found the explanation useful.
Regards.
Praseena.
|
|
|