Question 980808: A piece of 2m long wire is to be cut into two pieces one of which is to be formed into a circle and the other into an equilateral triangle. How should the wire be cut so that the total area enclosed is (a) a minimum and (b) a maximum
Answer by josgarithmetic(39632)   (Show Source): (Show Source):
You can put this solution on YOUR website! Cut into pieces x and y.
 . .
The circle:
 , because the length x now is used as the circumference. , because the length x now is used as the circumference.

-
area of this circle, 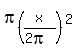
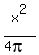
The equilateral triangle:
Perimeter is y.
This triangle composed of side  , and there are two associated 30-60-90 triangles making the equilateral triangle, with short leg , and there are two associated 30-60-90 triangles making the equilateral triangle, with short leg 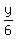 . Other leg will be the "height" of the equilateral triangle: . Other leg will be the "height" of the equilateral triangle:
-
h, the altitude.






-
Area of this equilateral triangle, 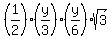 , ,
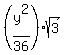
Total Area, 
Next is decide, do you want to substitute for x, or substitute for y?
-


-

MIN or MAX FOR FUNCTION, A:
Find derivative dA/dx, set equal to 0, solve for x. This should be straightforward if you already know how to do this from Calculus 1
(Placing graph of A(x) here):

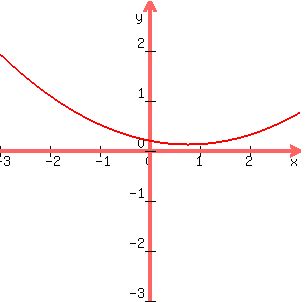
Expect a minimum at x slightly less than 1.
|
|
|