Question 980091: The area of a triangle is 39 square ft. The length of one side is 1 ft more than teice the altitude to that side. Find the length of that side and the altitude to the side.
Found 3 solutions by josgarithmetic, josh_jordan, MathTherapy:
Answer by josgarithmetic(39617)   (Show Source):
Answer by josh_jordan(263)  (Show Source):
You can put this solution on YOUR website! To solve this, we first need to know the formula for the area of a triangle:
 , where A is Area, b is base (length of one side), and h is height (altitude)
We are told that the length of one side (base) is 1 ft more than twice the altitude. In other words b = 2h + 1
Now, let's replace b in our formula for the area of a triangle with 2h + 1, and A with 39, since that's the area of the triangle:
We can now solve for h (altitude). First, multiply both sides of this equation by 2, which will give us
(2h + 1)(h) = 39 x 2 -----> (2h + 1)(h) = 78
Next, multiply (2h + 1) by (h), giving us
Third, subtract 78 from both sides and enter a 0 on the right side of the equal sign:
Fourth, factor this quadratic equation, which will give us:
Fifth, set each set of parentheses equal to zero and solve for both values of h:
 -----> ----->
 ----->
Since the height of a triangle cannot be a negative number, we can discard -13/2. So, our altitude (height) is 6 feet.
To find our length (base), replace the h in 2h + 1 with 6 and compute:
 -----> ----->
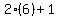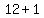Therefore, the length of this triangle is 13 feet and the altitude is 6 feet.
Answer by MathTherapy(10552)  (Show Source):
You can put this solution on YOUR website!
The area of a triangle is 39 square ft. The length of one side is 1 ft more than teice the altitude to that side. Find the length of that side and the altitude to the side.
Altitude:  ft
Other side (Base):  ft
|
|
|
