Question 948467: Locate the center, foci, vertices, ends of latera recta, & draw the ellipse. also compute the eccentricity & find the equation of the directices.
2.x^2/36+y^2/16=1
Answer by macston(5194)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
STANDARD FORM:

CENTER: Center is at (h,k) in this case (0,0). Center is at origin.
FOCI: Focus is (f) from center 
 Find square root of each side. Find square root of each side.

Foci are at (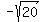 , , ) and ( ) and ( , , ). ).
VERTICES: In this case at (+ or - a,0) and a=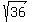 =6 =6
Vertices at (-6,0) and (6,0)
ENDPOINTS OF LATERA RECTA: The latera recta are perpendicular to the major axis at the foci, and have length: 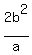 . Since half is above and half is below the axis, we need half the length or . Since half is above and half is below the axis, we need half the length or 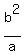 =16/6=8/3 =16/6=8/3
For the focus at (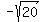 ), ), ), the endpoints of the latus rectum are ( ), the endpoints of the latus rectum are (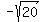 , ,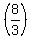 ) and ( ) and (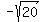 , ,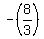 ) )
For the focus at ( , , ), the endpoints of the latus rectum are ( ), the endpoints of the latus rectum are ( , ,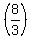 ) and ( ) and ( , ,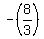 ) )
ECCENTRICITY: Eccentricity  =f/a= =f/a=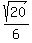
EQUATIONS OF DIRECTRICES: directrix is a line perpendicular to the main axis
on opposite the vertex from the focus, and same distance as the focus from the vertex. The directrix is outside the ellipse. The is a+(a-f) from the center,
or in this case, the directrix to the right of the origin is x=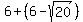 = =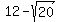 and to the left of the origin x=-( and to the left of the origin x=-(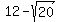 ). ).
|
|
|