Question 948466: Locate the center, foci, vertices, ends of latera recta, & draw the ellipse. also compute the eccentricity & find the equation of the directices.
1. 9x^2+25y^2=225
Answer by macston(5194)   (Show Source): (Show Source):
You can put this solution on YOUR website!  Divide each side by 225 Divide each side by 225


STANDARD FORM FOR ELLIPSE:
 NOTE: The largest denominator is always a, the other b. Since the a is under the x term, the major axis is horizontal. NOTE: The largest denominator is always a, the other b. Since the a is under the x term, the major axis is horizontal.
A). CENTER:Center is at (h,k) in this case (0,0)
B). FOCI:
(f) is distance from center to focus: 
 find the square root of each side find the square root of each side
f=+4 or -4
ANSWER: The foci are at (4,0) and (-4,0)
C). VERTICES:END POINTS OF MAJOR AXIS:
+ or - a is the distance from center: a=5 so:
ANSWER: Vertices are at (5,0) and (-5,0)
D). END POINTS OF LATERA RECTA:
The latera recta are perpendicular to the major axis at the foci,
the length given by 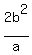 Since the focus is the midpoint, we use half this value Since the focus is the midpoint, we use half this value 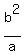 , in this case (9/5) , in this case (9/5)
ANSWERS:
The latus rectum at focus (4,0) has endpoints (4,9/5) and (4,-9/5)
The latus rectum at focus (-4,0) has endpoints (-4,9/5) and (-4,-9/5)
ECCENTRICITY:e=f/a=4/5 ANSWER e=eccentricity=4/5
EQUATIONS OF THE DIRECTRICES: 2a-f on major axis: 2a-f=10-4=6
ANSWERS:
Equation of directrix right of the origin: x=6
Equation of directrix left of the origin: x=-6
|
|
|