SOLUTION: The geometric mean of 2 positive numbers is the positive square root of their product. Find two consecutive positive even integers whose geometric mean is 2*square root sign*30

Algebra ->  Customizable Word Problem Solvers  -> Geometry -> SOLUTION: The geometric mean of 2 positive numbers is the positive square root of their product. Find two consecutive positive even integers whose geometric mean is 2*square root sign*30      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 933340: The geometric mean of 2 positive numbers is the positive square root of their product. Find two consecutive positive even integers whose geometric mean is 2*square root sign*30
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
Let the two consecutive positive even integers be n and n%2B2 .
our first equation is sqrt%28n%28n%2B2%29%29=2sqrt%2830%29 .
Squaring both sides of the equal sign, we get the equation
n%28n%2B2%29=%282sqrt%2830%29%29%5E2 ,
which has all the solutions of the original equation.
(It may have other extra solutions, that we call "extraneous solutions",
but we will check out all solutions at the end, and we will eliminate any extraneous solution then).

Solving:
n%28n%2B2%29=%282sqrt%2830%29%29%5E2
n%5E2%2B2n=4%2A30
n%5E2%2B2n=120<--->n%5E2%2B2n-120=0
The last equations above are two different versions of the same quadratic equation.
For this particular quadratic equation, there are 3 easy methods to solve it:
"completing the square",
factoring, and
using the "quadratic formula".
It seems to me that in this particular case "completing the square" is the easiest way to the solution, and this is how it goes.
n%5E2%2B2n=120
n%5E2%2B2n%2B1=120%2B1
%28n%2B1%29%5E2=121
%28n%2B1%29%5E2=11%5E2 ---> system%28n%2B1=11%2C%22or%22%2Cn%2B1=-11%29
Since we are looking for positive integers n and n%2B2 ,
n%2B1 must be a positive integer, so the only solution is
n%2B1=11 ---> n=11-1 ---> highlight%28n=10%29 .
So the two consecutive positive even integers area highlight%2810%29 and highlight%2812%29 , and
CHECKING we find that their geometric mean is sqrt%2810%2A12%29=sqrt%28120%29=sqrt%284%2A30%29=sqrt%284%29%2Asqrt%2830%29=2sqrt%2830%29

OTHER WAYS TO SOLVE THE SAME QUADRATIC EQUATION:
Using the quadratic formula:
The quadratic formula says that the solutions to a quadratic equation
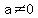ax%5E2%2Bbx%2Bc=0 , with a%3C%3E0 are given by
x+=+%28-b+%2B-+sqrt%28+b%5E2-4%2Aa%2Ac+%29%29%2F%282%2Aa%29+
In the case of n%5E2%2B2n-120=0 the coefficients are
a=1 , b=2 , and c=-120 , and the solutions will be given by
x+=+%28-2+%2B-+sqrt%28+2%5E2-4%2A1%2A%28-120%29+%29%29%2F%282%2A1%29+
x+=+%28-2+%2B-+sqrt%28+4%2B480%29%29%2F2
x=%28-2+%2B-+22%29%2F2 --->
Since -12 is not a positive even integer, we eliminate it, and then we check that x=10 is a solution to the problem, as done above.
Factoring:
n%5E2%2B2n-120=0--->%28n%2B12%29%28n-10%29=0--->system%28n%2B12=0%2C%22or%22%2Cn-10=0%29--->system%28n=-12%2C%22or%22%2Chighlight%28n=10%29%29
Since -12 is not a positive even integer, we eliminate it, and then we check that x=10 is a solution to the problem, as done above.