 The area of the square is 48 m²
So a side of the square is √48 = √16×3 = 4√3
AB is half a side of the square, so it's 2√3
OA is also 2√3
So by the Pythagorean theorem hypotenuse OB of right triangle OAB is
The area of the square is 48 m²
So a side of the square is √48 = √16×3 = 4√3
AB is half a side of the square, so it's 2√3
OA is also 2√3
So by the Pythagorean theorem hypotenuse OB of right triangle OAB is
 OB is the raius of the circle so by that formula for a circle's area:
OB is the raius of the circle so by that formula for a circle's area:
 Angle BDO is half of an interior angle of a regular hexagon. An
interior angle of a regular hexagon is given by:
Angle BDO is half of an interior angle of a regular hexagon. An
interior angle of a regular hexagon is given by:
 So angle BDO is 60°, so right triangle BDO is a 30°-60°-90°,
so its hypotenuse OD is twice BD. So by the Pythagorean theorem
So angle BDO is 60°, so right triangle BDO is a 30°-60°-90°,
so its hypotenuse OD is twice BD. So by the Pythagorean theorem






 BD is half a side of the hexagon, so one side of the
hgecagon is
BD is half a side of the hexagon, so one side of the
hgecagon is  , so the perimeter of the
hexagon is 6 times that, or
, so the perimeter of the
hexagon is 6 times that, or 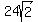 Edwin
Edwin