Question 898976: The length of the wall is 17m more than its width. If the area of the wall is less than 60m^2, what could be its possible length?
Answer by Jc0110(165)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let y to be the length, while z to be the width.
length, 
width, 
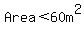

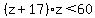
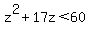
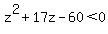
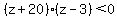
The range of z is 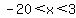 , which holds the number -19,-18,-17,-16,-15,-14,-13,-12,-11,-10,-9,-8,-7,-6,-5,-4,-3,-2,-1,0,1,2. , which holds the number -19,-18,-17,-16,-15,-14,-13,-12,-11,-10,-9,-8,-7,-6,-5,-4,-3,-2,-1,0,1,2.
Since the length for an area cannot be zero and in negatives, the range of z are 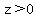 , , . .
To get the possible lengths, substitute  and and  into into  . .


or


Therefore, the possible lengths are 18m and 19m.
**In fact, the value z in range of 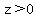 , , do not only include 1 and 2, but also involve the positive rational numbers, such as do not only include 1 and 2, but also involve the positive rational numbers, such as
0.00000...1, 0.001, 0.01, 0.1, 0.2, 0.26, 1.26895, 1.5, 1.55, 1.88888, 2.12, 2.563, 2.889, 2.9, 2.93, 2.99999999.
*As conclusion, value z can be any positive rational numbers as long as it is in this range: 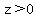 , , . .
|
|
|