SOLUTION: Would you please help me in finding the X in the following equation {{{ 40=(2X+8)(4X)(X) }}}

Click here to see ALL problems on Geometry Word Problems

Question 851785: Would you please help me in finding the X in the following equation

Found 2 solutions by ewatrrr, josh_jordan:
Answer by ewatrrr(24785) (Show Source):
You can put this solution on YOUR website!

Hi,
x = 1 is a root, can expand to find the other two roots
= = x^3 + 4x^2 - 5
Using Synthetic Division to Find other two roots
1 1 4 0 -5
1 5 5
1 5 5 0
(x^2 + 5x + 5)
X is -3.618, -1.382 , 1

Answer by josh_jordan(263) (Show Source):
You can put this solution on YOUR website!
The first step in solving for x, is to multiply each of the terms on the right of the equal sign. So, let's first multiply 2x + 8 by 4x. This gives us:

8x^2 + 32x

Now, multiply this result by x, which gives us:

8x^3 + 32x^2

We now have:

8x^3 + 32x^2 = 40

We can make this easier to solve by dividing each term by 8, since each term is divisible by 8. This gives us:

x^3 + 4x^2 = 5

Next, we can subtract 5 from both sides, giving us:

x^3 + 4x^2 - 5 = 0

Now, since we know that the only possible rational zeros are -1,1,5, or -5 (via the rational zero test), we can test each zero by plugging it into the equation to see if we end up with 0. If we plug -1,5, and -5 in for x, one at a time, we will not get 0 as our answer. However, plugging 1 in will give us 0. So, 1 is one of the values of x. We can use synthetic division or polynomial long division to divide x^3 + 4x^2 - 5 by x - 1 (because 1 is a value of x as we just discovered, and 1 in factor form is x - 1). When we divide, we are left with a quotient of:

x^2 + 5x + 5

If we set this equal to zero, we can use the quadratic formula to find our other two values of x:

----->

----->

We now have all of our values of x: , ,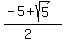