SOLUTION: isosceles trapezoid with a perimeter of 52 yards; the measure if one base is 10 yards greater than the other base, the measure of each leg is 3 yards less than twice the length of

Algebra ->  Customizable Word Problem Solvers  -> Geometry -> SOLUTION: isosceles trapezoid with a perimeter of 52 yards; the measure if one base is 10 yards greater than the other base, the measure of each leg is 3 yards less than twice the length of       Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 843854: isosceles trapezoid with a perimeter of 52 yards; the measure if one base is 10 yards greater than the other base, the measure of each leg is 3 yards less than twice the length of the shorter base, Find the area of the figure
Answer by josgarithmetic(39617) About Me  (Show Source):
You can put this solution on YOUR website!
A drawing helps, and is difficult to do through this system; so here is a description of the drawing:

Let b = the shorter base.
Longer base is b+10.
Each nonparallel side of the trapezoid is 2b-3, and the trapezoid has two of them.

The perimeter is then highlight_green%28b%2B%28b%2B10%29%2B%282b-3%29%2B%282b-3%29=52%29.
Omitting the steps,... the solution here is highlight%28b=8%29.
The smaller base is 8 yards and the larger base is 18 yards.

Each nonparallel side, -3%2B2%2A8=highlight%2813%29.

Relabeling all four sides of this trapezoid, you can figure how it is composed of a rectangle and two congruent right triangles. You want the HEIGHT of this entire figure. Continue analyzing this figure: the triangles each have 5 yard leg at the bottom, hypotenuse of 13, and unknown other leg, y.
We want this y, because this is the height of the figure:
highlight_green%28y%5E2%2B5%5E2=13%5E2%29.
y=sqrt%2813%5E2-5%5E2%29
y=sqrt%28169-25%29
y=sqrt%28144%29, ... highlight%28y=12%29.

AREA-------
(Average of the two bases) multiplied by (Altitude of the trapezoid)
Area, 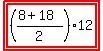highlight%28highlight%28%28%288%2B18%29%2F2%29%2A12%29%29
-
13*12=156 square yards