Question 832600: Find the slope of the bisector of the angle from L1 to L2. L1 passes through (-2,8) and (6,4), while L2 contains the points (0,12) and (-2,8)..
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! MY WAY:
A picture is worth a thousand words, but I am very wordy nonetheless.
We have point A(-2,8), point B(6,4), and point C(-2,8).
The rays L1 (AB) and L2 (AC) form angle BAC.
I drew all that in red below, and added a few extra items in green.
 Point D(2,16) is on ray L1 because AC and AD have the same slope. Point D(2,16) is on ray L1 because AC and AD have the same slope.
(It was easy to design it that way by making triangles CAX and DAY similar).
Point D(2,16) is at the same distance from A as point B.
(I know that because I made triangles DAY and ABZ congruent).
BAD is an isosceles triangle.BAD is an isosceles triangle.
(It is also a right triangle, but I don't care).
In isosceles triangle BAD, median AE is a median, an altitude, and a bisector of angle BAC.
(You must have been taught that about isosceles triangles in geometry class).
The slope of AE can be calculated from the coordinates of A and E.
E, being the midpoint of BD has the coordinates
 and and
 . .
The slope of AE is

ALTERNATE WAYS TO SOLVE IT:
THE HARDER WAY:
You could calculate the slope of AB and the slope of AC to get the tangents of the angles AB and AC make with the positive x-axis:
angle ZAB (measured as a negative angle, swept clockwise from AZ to AB), and
angle ZAC (measured as a positive angle, swept counterclockwise from AZ to AC).
You could average those angles to get the angle the bisector makes with the positive x-axis:
angle ZAE (measured as a positive angle, swept counterclockwise from AZ to AE).
Slope of AB = --> -->  (approximately, in radians) (or (approximately, in radians) (or 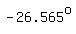 approximately, in degrees) approximately, in degrees)
Slope of AC = --> -->  (approximately, in radians) (or (approximately, in radians) (or  approximately, in degrees) approximately, in degrees)
  (approximately, in radians) (or (approximately, in radians) (or  approximately, in degrees) approximately, in degrees)
Then  = slope of AE (calculated approximsately). = slope of AE (calculated approximsately).
To calculate an exact value we need to use trigonometric identities to calculate
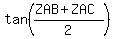 directly from directly from  and and 
AN EASIER WAY:
Realizing that the product of the lopes of AB and AC is  , we conclude that BAC is a right angle, , we conclude that BAC is a right angle,  . .
The angle the bisector makes with the positive x-axis must be 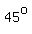 less than the angle AC makes with the positive x-axis. less than the angle AC makes with the positive x-axis.
We know the tangent of the angle AC makes with the positive x-axis,
 . .
We also know that 
So the slope of the bisector is

|
|
|