SOLUTION: what is the least number of square pieces into which a cardboard,13 ft long and 8 ft wide,can be cut?

Algebra ->  Customizable Word Problem Solvers  -> Geometry -> SOLUTION: what is the least number of square pieces into which a cardboard,13 ft long and 8 ft wide,can be cut?      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 830222: what is the least number of square pieces into which a cardboard,13 ft long and 8 ft wide,can be cut?
Answer by Edwin McCravy(20056) About Me  (Show Source):
You can put this solution on YOUR website!
Let the side of each square be x, where x is not necessarily a 
positive integer.  However there must be a positive integer N such that
Nx = 13.  And there must be another positive integer M such that Mx=8

And we want these positive integers N and M to be as small as possible.

So we have

Nx = 13
Mx = 8

Dividing equals by equals:

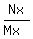
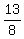Nx%2F%28Mx%29%22%22=%22%2213%2F8

Cancel the x's

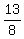N%2FM%22%22=%22%2213%2F8

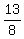Since 13%2F8 is in lowest terms, the smallest
integers N and M can be are N=13 and N=8, so the smallest
number of squares is to cut it up into 1 ft by 1 ft squares.

                           
| | | | | | | | | | | | | |
| | | | | | | | | | | | | |
| | | | | | | | | | | | | |
| | | | | | | | | | | | | |
| | | | | | | | | | | | | |
| | | | | | | | | | | | | |
| | | | | | | | | | | | | |
| | | | | | | | | | | | | |

Answer: 13×8 = 104.

Edwin