SOLUTION: I actually dont know if this is a geometry question but it has rectangles, perimeter, and area in it. (Sorry if I selected the topic wrong) Here is my question: A rectangle has

Algebra ->  Customizable Word Problem Solvers  -> Geometry -> SOLUTION: I actually dont know if this is a geometry question but it has rectangles, perimeter, and area in it. (Sorry if I selected the topic wrong) Here is my question: A rectangle has      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 825268: I actually dont know if this is a geometry question but it has rectangles, perimeter, and area in it. (Sorry if I selected the topic wrong)
Here is my question:
A rectangle has a perimeter of 40m and an area of 91m^2. If the length is longer than the width, find the length.
I dont know if my solution is right but i think it is absolutely wrong. Can you please correct me?
(This is what I understood about the problem)
perimeter of a rectangle = 40m
area of rectangle= 90m^2
( Perimeter of a rectangle is 2l+2w right? while area is l*w)
So I Put it this way
2l+2w= 40m
l*w= 90 m^2
That is what I tried I dont know what to do. Please help me on this one
Found 2 solutions by josgarithmetic, MathTherapy:
Answer by josgarithmetic(39617) About Me  (Show Source):
You can put this solution on YOUR website!
Not sure if you meant 90 m^2 or 91 m^2, but no big deal if you just recheck your problem description as it is given to you from your book or your document material.

The symbolic work you tried appears good. Why stuck? Maybe you tried using an incorrect value for the area?

x for length, w for width,
2x%2B2w=40, and xw=A for some constant area A.
from perimeter, divide left and right by 2, obtaining x%2Bw=20.
'
w=20-x.
xw=A
x%2820-x%29=A
20x-x%5E2=A
x%5E2-20x=-A
x%5E2-20x%2BA=0-------But you only need consider two possible choices for A.

My guess is that A=91. Why? highlight_green%2891=13%2A7%29, and then the quadratic expression might be factorable:

x%5E2-20x%2B91=0
%28x-7%29%28x-13%29=0
highlight%28x=7%29 or highlight%28x=13%29

One dimension will be 7 and the other dimension will be 13.

Answer by MathTherapy(10552) About Me  (Show Source):
You can put this solution on YOUR website!

I actually dont know if this is a geometry question but it has rectangles, perimeter, and area in it. (Sorry if I selected the topic wrong)
Here is my question:
A rectangle has a perimeter of 40m and an area of 91m^2. If the length is longer than the width, find the length.
I dont know if my solution is right but i think it is absolutely wrong. Can you please correct me?
(This is what I understood about the problem)
perimeter of a rectangle = 40m
area of rectangle= 90m^2
( Perimeter of a rectangle is 2l+2w right? while area is l*w)
So I Put it this way
2l+2w= 40m
l*w= 90 m^2
That is what I tried I dont know what to do. Please help me on this one


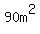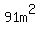You're correct up to that point, with the exception that the area is NOT 90m%5E2, but 91m%5E2.

I'll finish it for you!!

2L + 2W = 40____2(L + W) = 2(20)_____L + W = 20

L = 20 – W ----- eq (i)

LW = 91 -------- eq (ii) 

W(20 – W) = 91 ------- Substituting 20 – W for L in eq (ii)

20W+-+W%5E2+=+91

W%5E2+-+20W+%2B+91+=+0

(W - 7)(W - 13) = 0

W – 7 = 0		   OR			W – 13 = 0

W, or width = 7		   OR			W = 13



If W, or width = 7, then length = 13

If W, or width = 13, then length = 7



Since the width's measurement is less than that of the length's, then width is: highlight_green%287%29, and length is: highlight_green%2813%29

You can do the check!! 



Send comments, “thank-yous,” and inquiries to “D” at MathMadEzy@aol.com.

Further help is available, online or in-person, for a fee, obviously. 



For FREE info and answers to questions about the ASVAB exam, the NYS 3 – 8 city/state wide exams, 

GENERAL MATH QUESTIONS, MATH HOMEWORK QUESTIONS, or MATH QUESTIONS related to the Regents Integrated Algebra,

Regents Geometry, Regents Algebra 2/Trigonometry, SHSAT, COOP/HSPT/TACHS, PSAT, SAT, ACT, SSAT/ISEE, GRE, CLEP,

and the GED, you can visit: http://asvabstudyzone.freeforums.net/.