Question 766846: In ABC , a=22cam,b=19cm and ABC =55 degrees. Sketch the triangle and solve the triangle. Round answers to the nearest tenth.
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
You can put this solution on YOUR website!
 This is a problem of the AMBIGUOUS case SSA, (side-side-angle)
where you are asked to solve a triangle given two sides and a
non-included angle. If I have drawn this triangle accurately
to scale, then it appears that there are two solutions to
this problem. If we open a compass to 19 units, put the sharp
point of the compass at C and swing an arc, like this,
This is a problem of the AMBIGUOUS case SSA, (side-side-angle)
where you are asked to solve a triangle given two sides and a
non-included angle. If I have drawn this triangle accurately
to scale, then it appears that there are two solutions to
this problem. If we open a compass to 19 units, put the sharp
point of the compass at C and swing an arc, like this,
   So it appears that there are two solutions, these two triangles:
So it appears that there are two solutions, these two triangles:
  We will use the law of sines to determine angle A
We will use the law of sines to determine angle A
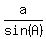  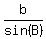 bĚsin(A) = aĚsin(B)
sin(A) =
bĚsin(A) = aĚsin(B)
sin(A) = 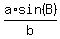 sin(A) =
sin(A) =  sin(A) = 0.948918408 <--- If this had been greater than 1, there
would have been no solution. If this had
been exactly 1, there would have been 1 right
triangle angle solution. But since it is less
than 1, we can tell that there is either 1 or 2
solutions.
If you use your calculator with the inverse sine,
you get
A = 71.5303934░.
That is a correct value for angle A. However there is another
possible angle with that same sine, which is a second quadrant
angle, and it is found by subtracting A = 71.5303934░ from 180░.
We will use primes on the letters to indicate the possible
second solution:
A' = 180░ - 71.5303934░ = 108.4696066░
So we put those two values in:
First solution Second solution (maybe)
A = 71.5303934░ A' = 108.4696066░
B = 55░ B' = 55░
C = C' =
a = 22 a' = 22
b = 19 b' = 19
c = c' =
To find out whether there are 2 solutions or only 1,
we calculate the angles C and C', and see if both
are possibilities:
We calculate C by using 180░-A-B = 180░-71.5303934░-55░ = 53.4696066░
We calculate C' by using 180░-A'-B' = 180░-108.4696066░-55░ = 16.5303934░
Since C' came out positive, we know that there are two solutions,
[If C' had come out negative, there would have been only 1 solution].
First solution Second solution
A = 71.5303934░ A' = 108.4696066░
B = 55░ B' = 55░
C = 53.4696066░ C' = 16.5303934░
a = 22 a' = 22
b = 19 b' = 19
c = c' =
Now we just have to calculate sides c and c'
To calculate side c:
sin(A) = 0.948918408 <--- If this had been greater than 1, there
would have been no solution. If this had
been exactly 1, there would have been 1 right
triangle angle solution. But since it is less
than 1, we can tell that there is either 1 or 2
solutions.
If you use your calculator with the inverse sine,
you get
A = 71.5303934░.
That is a correct value for angle A. However there is another
possible angle with that same sine, which is a second quadrant
angle, and it is found by subtracting A = 71.5303934░ from 180░.
We will use primes on the letters to indicate the possible
second solution:
A' = 180░ - 71.5303934░ = 108.4696066░
So we put those two values in:
First solution Second solution (maybe)
A = 71.5303934░ A' = 108.4696066░
B = 55░ B' = 55░
C = C' =
a = 22 a' = 22
b = 19 b' = 19
c = c' =
To find out whether there are 2 solutions or only 1,
we calculate the angles C and C', and see if both
are possibilities:
We calculate C by using 180░-A-B = 180░-71.5303934░-55░ = 53.4696066░
We calculate C' by using 180░-A'-B' = 180░-108.4696066░-55░ = 16.5303934░
Since C' came out positive, we know that there are two solutions,
[If C' had come out negative, there would have been only 1 solution].
First solution Second solution
A = 71.5303934░ A' = 108.4696066░
B = 55░ B' = 55░
C = 53.4696066░ C' = 16.5303934░
a = 22 a' = 22
b = 19 b' = 19
c = c' =
Now we just have to calculate sides c and c'
To calculate side c:
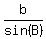 = = 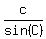
 = =  cĚsin(55░) = 19Ěsin(53.4696066░)
c =
cĚsin(55░) = 19Ěsin(53.4696066░)
c =  c = 18.63791123
---
To calculate side c':
c = 18.63791123
---
To calculate side c':
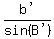 = = 
 = =  c'Ěsin(55░) = 19Ěsin(16.5303934░)
c' =
c'Ěsin(55░) = 19Ěsin(16.5303934░)
c' =  c' = 6.599451972
So we end up with:
First solution Second solution
A = 71.5303934░ A' = 108.4696066░
B = 55░ B' = 55░
C = 53.4696066░ C' = 16.5303934░
a = 22 a' = 22
b = 19 b' = 19
c = 18.63791123 c' = 6.599451972
Incidentally the drawings above are to scale,
because I calculated them before drawing them.
You can round the solutions to tenths.
A = 71.5░ A' = 108.5░
B = 55░ B' = 55░
C = 53.5░ C' = 16.5░
a = 22 a' = 22
b = 19 b' = 19
c = 18.6 c' = 6.6
However, you should wait until the end to round off
because if you round earlier, the answers will likely
be too inaccurate.
Edwin
c' = 6.599451972
So we end up with:
First solution Second solution
A = 71.5303934░ A' = 108.4696066░
B = 55░ B' = 55░
C = 53.4696066░ C' = 16.5303934░
a = 22 a' = 22
b = 19 b' = 19
c = 18.63791123 c' = 6.599451972
Incidentally the drawings above are to scale,
because I calculated them before drawing them.
You can round the solutions to tenths.
A = 71.5░ A' = 108.5░
B = 55░ B' = 55░
C = 53.5░ C' = 16.5░
a = 22 a' = 22
b = 19 b' = 19
c = 18.6 c' = 6.6
However, you should wait until the end to round off
because if you round earlier, the answers will likely
be too inaccurate.
Edwin
|
|
|