SOLUTION: Question: The Hypotenuse of a right triangle exceeds the longer of the two legs by 2. If the perimeter of the triangle is 40, find the lengths of the sides of the triangle. I

Algebra ->  Customizable Word Problem Solvers  -> Geometry -> SOLUTION: Question: The Hypotenuse of a right triangle exceeds the longer of the two legs by 2. If the perimeter of the triangle is 40, find the lengths of the sides of the triangle. I      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 75820: Question: The Hypotenuse of a right triangle exceeds the longer of the two legs by 2. If the perimeter of the triangle is 40, find the lengths of the sides of the triangle.
I came up with the answer, but I have to show an algebraic solution which I did not do.
Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!
Let c=hypotenuse, a=longer leg, b=other leg
Since the hypotenuse exceeds the longer leg by 2, it is 2 units more than the longer leg. In other words:
c=a%2B2
Since the perimeter is 40, we can find the other leg by the perimeter formula
P=a%2Bb%2Bc where P is the perimeter and a,b,c, are the sides of the triangle
40=a%2Bb%2Bc
40=a%2Bb%2B%28a%2B2%29 Substitute a+2 into c
Since the missing side (b) can be found by Pytagoreans Thereom, we can say
a%5E2%2Bb%5E2=c%5E2
b%5E2=c%5E2-a%5E2
b=sqrt%28c%5E2-a%5E2%29 Solve for b
b=sqrt%28%28a%2B2%29%5E2-a%5E2%29 Substitute a+2 into c
b=sqrt%28a%5E2%2B4a%2B4-a%5E2%29
b=sqrt%284a%2B4%29
Now plug in 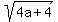sqrt%284a%2B4%29 in for b to complete the equation
40=a%2Bsqrt%284a%2B4%29%2B%28a%2B2%29
40=2a%2B2%2Bsqrt%284a%2B4%29
38-2a=sqrt%284a%2B4%29
%2838-2a%29%5E2=%28sqrt%284a%2B4%29%29%5E2 Square both sides
4a%5E2-156a%2B1444=4a%2B4
4a%5E2-148a%2B1440=0 Get all terms to one side
Now plug your quadratic into the quadratic formula to find a (sorry the solver wouldn't format):
if we use a calculator, we get:
a=24 or a=15
Now lets find c
c=a%2B2
c=24%2B2 Let a=24
c=26
Since 24+26=50 which is over 40, 24 is not our answer
c=a%2B2
c=15%2B2 Let a=24
c=17
Now find b
b=sqrt%28c%5E2-a%5E2%29
b=sqrt%2817%5E2-15%5E2%29
b=sqrt%28289-225%29
b=sqrt%2864%29
b=8
So the sides are:
a=15,b=8,c=17


Check:
40=a%2Bb%2Bc Use the perimeter formula to check
40=15%2B8%2B17 Plug in a=15,b=8,c=17
40=40 works