Question 726188: how do you find the length of a leg of right triangle given hypotenuse and the angles?
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! You use the trigonometric ratios
For most angles, you would let your calculator figure out the values of the sine and cosine of that angle. Fifty to forty years ago, we used tables from books, or slide rules.
Sine and cosine of some angles can be calculated more easily.
A right triangle with acute angles measuring  and  is half of an equilateral triangle. If the length of the short leg (opposite the angle) is  , the length of the hypotenuse will be  . and according the the Pythagorean theorem, the length of the other leg,  , will be
 .
So, from the point of view of the angle,
 and  and
from the point of view of the angle,
 and 
Ina any case, the legs of a right triangle with acute angles measuring and are as long as
 and  times the length of the hypotenuse.
A right triangle with both acute angles measuring 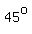 is an isosceles right triangle. Its legs, being opposite angles with equal measure, have equal lengths. Such a triangle is half of a square, and the legs can be proven to be  times as long as the hypotenuse.
 The Pythagorean theorem says that 
Then -->  -->  -->  -->  --> 
|
|
|
