Looking at the expression  , we can see that the first coefficient is , we can see that the first coefficient is  , the second coefficient is , the second coefficient is  , and the last term is , and the last term is  . .
Now multiply the first coefficient  by the last term by the last term  to get to get  . .
Now the question is: what two whole numbers multiply to  (the previous product) and add to the second coefficient (the previous product) and add to the second coefficient  ? ?
To find these two numbers, we need to list all of the factors of  (the previous product). (the previous product).
Factors of  : :
1,2,3,4,5,6,10,12,15,20,30,60
-1,-2,-3,-4,-5,-6,-10,-12,-15,-20,-30,-60
Note: list the negative of each factor. This will allow us to find all possible combinations.
These factors pair up and multiply to  . .
1*60 = 60
2*30 = 60
3*20 = 60
4*15 = 60
5*12 = 60
6*10 = 60
(-1)*(-60) = 60
(-2)*(-30) = 60
(-3)*(-20) = 60
(-4)*(-15) = 60
(-5)*(-12) = 60
(-6)*(-10) = 60
Now let's add up each pair of factors to see if one pair adds to the middle coefficient  : :
| First Number | Second Number | Sum | | 1 | 60 | 1+60=61 | | 2 | 30 | 2+30=32 | | 3 | 20 | 3+20=23 | | 4 | 15 | 4+15=19 | | 5 | 12 | 5+12=17 | | 6 | 10 | 6+10=16 | | -1 | -60 | -1+(-60)=-61 | | -2 | -30 | -2+(-30)=-32 | | -3 | -20 | -3+(-20)=-23 | | -4 | -15 | -4+(-15)=-19 | | -5 | -12 | -5+(-12)=-17 | | -6 | -10 | -6+(-10)=-16 |
From the table, we can see that there are no pairs of numbers which add to  . So . So  cannot be factored. cannot be factored.
===============================================================
Answer:
So 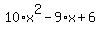 doesn't factor at all (over the rational numbers). doesn't factor at all (over the rational numbers).
So 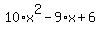 is prime. is prime.
|