Question 608993: The second angle in a triangle is one third as the large as the first. The third angle is two thirds as large as the first angle. Find the angle measures. -So this is the question, I've tried different things but I was supposed to get =180 since its a triangle and I'm a bit confused ! Please and thank you.
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! As with many word problems you need variables, expressions involving these variables, and one or more equations involving these expressions.
The number of variables you use determines the number of equations you need: 1 variable needs 1 equation, 2 variables need two equations, etc. So the fewer variables you use, the fewer equations you will need to come up with. Since the problem describes both the second and third angles in terms of the first angle, it will be possible to use just one variable (and one equation) to solve this problem.:
Let x = the measure of the first angle.
To express the second angle we must translate "The second angle ...is one third as the large as the first." Since "one third as large as" means the same thing as "one third of" and since fractions of something translates into the fraction times the something we get:
The second angle is 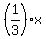 . .
Next we translate "The third angle is two thirds as large as the first angle". Using logic similar to what we used to get an expression for the second angle we should find that:
The third angle is 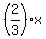
We now have expressions for the three angles. We used only one variable so we only need one equation. The equation will come from the fact that the three angles of any triangle add up to 180. So
The first angle plus the second angle plus the third angle equals 180. Translating this sentence into an equation, using our expressions for the three angles we get:

Now that we have an equation we use algebra to solve it. First we simplify. 





Dividing by two we get:
x = 90.
Since "x" represented the first angle, the first angle is 90 degrees. Since 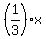 was the second angle and since x = 90, the second angle is was the second angle and since x = 90, the second angle is  . And since the third angle was . And since the third angle was 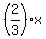 we get we get  for the third angle. for the third angle.
In summary,
The first angle = 90
The second angle = 30
The third angle = 60
|
|
|