Question 589248: A wooden pyramid, 9 inches tall, has a square base. A carpenter increases the dimensions of the wooden pyramid by a factor of 4 and makes a larger pyramid with the new dimensions. Describe in complete sentences the ratio of the volumes of the two pyramids.
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! The ratio of the volmes of similar solids, is the cube of the ratio of its linear dimensions. In this case that ratio would be  .
If we did not know that, we would know that the volume of a pyramid with a height of 9 inches, and a sqare base of side length x inches is, in cubic inches,
A larger pyramid, enlargerd by a factor of 4, would have a height of 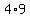 inches, a base side length of  inches, and a volume, incubic inches, of
|
|
|
