Question 570724: The town of Foxton lies 10 mi north of an abandoned east-west road that runs through Grimley, as shown in the figure. The point on the abandoned road closest to Foxton is 60 mi from Grimley. County officials are about to build a new road connecting the two towns. They have determined that restoring the old road would cost $100,000 per mile, while building a new road would cost $200,000 per mile. How much of the abandoned road should be used (as indicated in the figure) if the officials intend to spend exactly $8.8 million?
How much would it cost to build a new road connecting the towns directly? (Round your answer to one decimal place.)
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! The town of Foxton lies 10 mi north of an abandoned east-west road that runs through Grimley, as shown in the figure.
The point on the abandoned road closest to Foxton is 60 mi from Grimley.
County officials are about to build a new road connecting the two towns.
They have determined that restoring the old road would cost $100,000 per mile, while building a new road would cost $200,000 per mile.
How much of the abandoned road should be used (as indicated in the figure) if the officials intend to spend exactly $8.8 million?
:
This is a triangle problem has a right angle at a point on the old road directly south of Fox
:
Leg 1 = 10 mi
leg 2 = x, the distance from a point due south of F, to where the new road joins the old road
hypotenuse = new road distance
(60-x) = restored road distance
then
Road dist from F to G = hypotenuse + (60-x)
:
Cost: hypotenuse 200,000 per mile; (60-x) $100,000 per mile
:
Do this in 100 thousands of dollars, to avoid writing all these zeros
:
New road cost + old road cost = 8.8 million
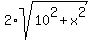 + 1(60-x) = 88 + 1(60-x) = 88
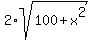 = 88 - (60-x) = 88 - (60-x)
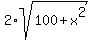 = 88 - 60 + x = 88 - 60 + x
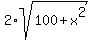 = x + 28 = x + 28
Square both sides
4(100+x^2) = (x+28)^2
400 + 4x^2 = x^2 + 56x + 784
Combine like terms on the left
4x^2 - x^2 - 56x + 400 - 784 = 0
3x^2 - 56x - 384 = 0
we can use the quadratic formula here, but this will factor to:
(x-24)(3x+16) = 0
The positive solution
x = 24
then
New road construction dist:
 = 26 mi = 26 mi
:
Old road restored dist:
60 - 24 = 36 mi
:
If we did this right, the cost should be 8.8 million
26(200000) = $5,200,000
36(100000) = $3,600,000
------------------------
total road: $8,800,000 which is 8.8 million
:
:
How much would it cost to build a new road connecting the towns directly?
(Round your answer to one decimal place.)
That would be the hypotenuse again, only this time:
Cost = 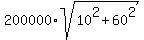 = $12,165,525 = $12,165,525
:
How about this? Did all this make sense to you?
|
|
|