Question 548213: An open box is formed by cutting a 8 inch square measured from each corner and folding up the sides. If the volume of the carton is then 64 in3, what was the length of a side of the original square of cardboard?
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! The original square of cardboard, with the cutting and folding lines would look like this:
 Cutting lines are red, folding lines are blue.
You see 4 congruent squares cut out of the corners. If the length of the sides of those squares is 8 inches, then the height of the box will be 8 inches.
Let x be the length (in inches) of the side of the blue square (the bottom of the box).
The surface area of the bottom (in square inches) is  ,
and the volume of the box, calculated as area of the bottom times height, (in cubic inches) is
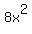
So  --->  --->  or about 2.83 inches.
(That is going to be a tall box with a very narrow base, too easily tipped over.
I would have cut squares with side length 4 inches from the corner, and that would have given me a nice cube.)
So if the length of the side of the base is 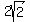 , with 8 inches of length added to each side, the length of the side of the original cardboard square must have been  , or about 18.83 inches.
I still think we should have made a cubic box with 4 inch sides by cutting squares with 4 inch sides from a 12 inch by 12 inch square of cardboard. It would have used less material, wasted less material in the cutouts, for a box with the same volume, less surface, and much better stability.
|
|
|
