One diagonal of a rhombus is 14 units and the area of the rhombus is 63 square
units. How long is the other diagonal? How long is each side?
This is the rhombus with the given diagonal:
Let the 4 sides be x units each:
 Since the diagonals of a rhombus are perpendicular bisectors
of each other, the other diagonal, shown in green below divides
the 14 unit diagonal into two halves, 7 units each. Let each half
of the green diagonal be y units each:
Since the diagonals of a rhombus are perpendicular bisectors
of each other, the other diagonal, shown in green below divides
the 14 unit diagonal into two halves, 7 units each. Let each half
of the green diagonal be y units each:
 The rhombus is divided into 4 congruent right triangles.
Let's look at just one of those 4 right triangles, say
the upper left one:
The rhombus is divided into 4 congruent right triangles.
Let's look at just one of those 4 right triangles, say
the upper left one:
 It's area is
It's area is  th of the area of the entite
rhombus, so its area is
th of the area of the entite
rhombus, so its area is 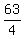 .
Since the area of a triangle is given by the formula:
Area =
.
Since the area of a triangle is given by the formula:
Area =  ×base×height
The Area is
×base×height
The Area is 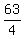 . the base is 7, and the height
is y.
. the base is 7, and the height
is y.
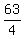 =
=  ·7·y
Multiply both sides by 4 to clear of fractions:
63 = 2·7·y
63 = 14y
·7·y
Multiply both sides by 4 to clear of fractions:
63 = 2·7·y
63 = 14y
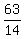 = y
= y
 = y
The hypotenuse x can be found by the Pythagorean theorem
x² = 7² + y²
x² = 49 +
= y
The hypotenuse x can be found by the Pythagorean theorem
x² = 7² + y²
x² = 49 +  ²
x² = 49 +
²
x² = 49 + 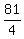 x² =
x² = 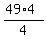 +
+ 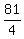 x² =
x² = 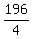 +
+ 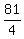 x² =
x² = 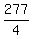 x =
x = 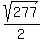 So back to the original rhombus,
So back to the original rhombus,
 The length of the green diagonal is 2y or 2×(
The length of the green diagonal is 2y or 2×( ) = 9 units
Each side of the rhombus is x or
) = 9 units
Each side of the rhombus is x or 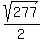 Edwin
Edwin