Question 495218: Please help me solve the word problem using
The Rational Zero Theorem
An open metal tank is to be made from a rectangular piece of stainless steel that measures 12 by 6 feet, by cutting out squares of the same size from each corner and bending up the sides. If the volume of the tank is to be 50 ft^3 , how large the square should be cut from each corner?
Answer by Theo(13342)   (Show Source):
You can put this solution on YOUR website! well, i didn't solve your problem for you, although, in a sense i did.
the reason is that the problem doesn't have a solution for any of the dimensions being all greater than 0.
here's what i did.
your piece of steel has a length of 12 feet and a width of 6 feet.
you want to cut off a square from each end and then fold up the sides to make a tank that will have a volume of 50 cubic feet.
your tank will have a height, a length, and a width.
we will let x represent the height.
x also represents the side of the square that will be removed from each corner of your rectangle.
the length of the tank will be represented by 12 - 2x because x is cut off the length from both ends.
the width of the tank will be represented by 6 - 2x because x is cut off the width from both ends.
the picture below shows you what i mean.
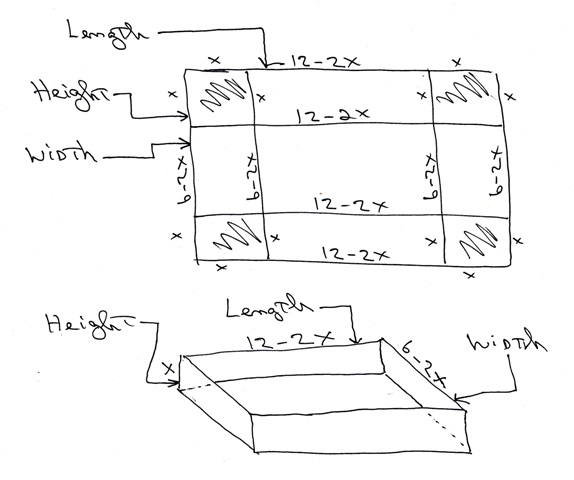
before going through the drill of trying to find the factors, i drew a graph of the equation that gave me the volume of the tank.
the formula for that volume is:
L * W * H = V
V = volume
L = length
W = width
H = height.
the height is equal to x.
the length is equal to 12 - x
the width is equal to 6 - x
the equation that i got was:
V = L * W * H which became:
V = (12 - 2x) * (6 - 2x) * x
since V = 50, this equation became:
(12 - 2x) * (6 - 2x) * x = 50
to graph this equation, i subtracted 50 from both sides of the equation and then set the equation equal to y to get:
y = (12 - 2x) * (6 - 2x) * x - 50
when y = 0, i have a solution to this equation.
when y = 0 this equation becomes:
(12 - 2x) * (6 - 2x) * x - 50 = 0
if you add 50 to both sides of this equation, then you get:
(12 - 2x) * (6 - 2x) * x = 50
this is exactly the equation for the volume of the tank.
so, when y = 0, this equation has a solution for the volume of the tank.
to see when y = 0, i graphed the equation of y = (12 - 2x) * (6 - 2x) * x - 50.
the graph that i got is shown below:
while this provides a solution, the solution is not valid.
it is not valid because:
when x = 6.5:
L = (12 - 2x) = (12 - 13) = -1
W = (6 - 2x) = (6 - 13) = -7
H = 6.5
V = 6.5 * (-1) * (-7) = 45.5
the actual value of x that gets us close to a volume of 50 is 6.53993479
that doesn't matter.
what matters is that the dimensions of the tank are negative which can't be.
what this means is we don't have a solution to this problem where the length and the width and the height are all positive.
so the answer to the problem is that there is no solution that is possible based on the requirements of the equation.
you can have a tank with a volume of 50 cubic feet.
for example:
a length of 5 and a width of 5 and a height of 2 will get you a tank with a volume of 50 cubic feet.
similarly, a length of 5 and a width of 2.5 and a height of 4 will get you a tank with a volume of 50 cubic feet.
these will not, however, fit the requirements of the equation which was that a square had to be cut out of the ends of the rectangle that were all the same size, and the rectangle had to be 12 by 6 to start with.
please also not that the solution is not an integer, nor is it a rational number as far as i can tell.
i checked the rational zero theorem.
from that, the possible answers that could be are:
50 = 1 * 50 or 2 * 25 or 5 * 10 = p
4 = 1 * 4 or 2 * 2 = p
p/q = 50 or 50/4 or 50/2 or 25 or 25/4 or 25/2 or 5 of 5/4 or 5/2 or 10 or 10/4 or 10/2
these can be simplified to 50 or 25 or 5 or 10 or 12.5 or 6.25 or 2.5 or 1.25
none of these turned out to be rational factors of the equation.
if you want to learn how to find the rational factors of an equation, then this reference might be helpful:
http://www.sparknotes.com/math/algebra2/polynomials
/section4.rhtml
i have solved problems like this before and they have had solutions. this particular equation, however, doesn't.
not as far as i can tell.
the graph pretty much tells the whole story.
if the equation is correct (and i believe that it is), the graph shows you there is only one solution to this problem and that solution is not a viable one because it leads to negative lengths and widths.
you can still get a positive volume, because a minus times a minus equals a plus, but that doesn't help. the individual lengths and widths both have to be positive.
|
|
|
