Question 477556: A square has an area of x^2 + 6x + 9 find the length of a side. Make a sketch of the square Please help
Found 5 solutions by htmentor, tinbar, Theo, richard1234, ikleyn:
Answer by htmentor(1343)   (Show Source): (Show Source):
You can put this solution on YOUR website! A square has an area of x^2 +6x+9 find teh length of a side. Make a sketch of the square
===========================================
The expression for the area can be factored as:
x^2 + 6x + 9 = (x+3)(x+3)
So each side has length x+3
Answer by tinbar(133)   (Show Source): (Show Source):
You can put this solution on YOUR website! First of all, you will certainly agree that a square has 4 sides, and that all 4 sides are equal in length. Also, if you are not already aware, the area of a square is all the space bounded by those 4 sides. The formula for the area is length times width, where the length is the size of a vertical side, while the width is the size of a horizontal side. However, since all sides are equal, the area is equal to the size of any side times itself(length squared, or width squared)
So, now we are given that some square has area x^2 +6x+9. What ever the length of a side is, when you multiply it by itself we should get x^2 +6x+9.
? * ? = x^2 +6x+9.
Now, directly taking the square root of a polynomial (such as x^2 +6x+9), is not necessarily obvious, or easy. So let's try to guess as wisely as we can.
( )*( ) = x^2 +6x+9
We need to fill the brackets and we have our answer, and note, whatever we do to one bracket, we must do to the other, since a square as equal sides, meaning the length and width have to be the same 'quantity.'
Let's start with x in the first bracket, immediately we get x in the second one, since we have to do the same to each bracket.
(x )*(x ) = x^2 +6x+9. We choose x, since x*x=x^2, so at least we get our first term. Now we notice the last term is 9, and that 9 is 3^2., so let's put a +3 in each bracket since 3*3=9. Doing this guarantees our last term, but there's going to be a middle term, let's hope it turns out to be 6x!
now we want to check what (x+3)*(x+3) actually expands into. If you are not familiar with these expansions, here's a general example that should explain it well enough to understand and solve this problem. If we have some (a+b)*(c+d), where a,b,c,d can be variables, or numbers, or anything really, then the expansion of (a+b)*(c+d) = (a*c)+(a*d)+(b*c)+(b*d); I believe this is known as the foil method.
Back to our problem, (x+3)*(x+3)=x^2+3x+3x+9 according to the formula. The two middle terms 3x, 3x can be added up since they are 'like' terms. 3x+3x = 6.
Therefore, (x+3)*(x+3) = x^2 +6x+9 meaning the length of side is x+3 units.
For the graph, along the x axis (y=0), plot some point and label that point (x,0). Then, from that labeled points, move 3 "units"(which can be cm, or whatever scale you are using), to the right and plot that point as (x+3,0). Then from the (x,0) point move 3 units up, and label that (x,3). Finally plot and label a point at (x+3,3)(I'll leave it to you to figure out how to find where this last point is on the graph). Once you have the 4 points, connect them, and that's a graph of the square.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the area of a square is equal to s*s = s^2
s = 1 side of the square.
the area of the square is equal to x^2 + 6x + 9
this means that s^2 = x^2 + 6x + 9
this means that s = sqrt(x^2 + 6x + 9)
it just so happens that x^2 + 6x + 9 is a perfect square.
it is equal to (x+3)^2
this means that s^2 = (x+3)^2 which means that:
sqrt(s^2) = +/- sqrt(x+3)^2 which means that:
s = +/- (x+3)
if s = + (x+3) then:
s = x + 3
if s = -(x+3) then:
s = -x - 3
now s has to be > 0.
this means that:
x+3 > 0 which means that x > -3
this also means that:
-x-3 > 0 which means that x < -2
this means that x can be any real number except -3.
when x is equal to -3, s is equal to 0 and the area of the square is equal to 0 which means that you don't have a square of any magnitude.
the length of each side of your square is dependent on the value of x.
a graph of the equation of x^2 + 6x + 9 is shown below:
this graph shows the area of the square based on the value of x.

regardless of the value of x, this graph will be positive which means the area of the square will be positive.
this is everywhere except when x = -3.
when x = -3, the area is zero which we already indicated is not valid.
each side of your square, however, is not fixed to any one length.
the length of each side is dependent on the value of x.
a graph of the equation of y = +/- sqrt(x^2 + 6x + 9)}}} is shown below:
this graph is showing the value of the side of the square based on the value of x.

you can see that the length of each side will always be positive.
it's low point is 0 when x = -3, which is disallowed.
you asked me to draw your square.
any square will do.
just draw a rectangle which has all sides equal to each other.
each side of this square will be equal to sqrt(x^2 + 6x + 9).
x can be any value except -3.
you can also show the value of each side of the square as follows:
s = absolute value of (x+3).
in formula terms, this looks like:
s = |x+3|
when (x+3) is positive, you get s = x + 3
when (x+3) is negative, you get s = -(x + 3) which becomes s = -x - 3.
these are the same values we calculated above.
as ugly as it might look, that's your answer.
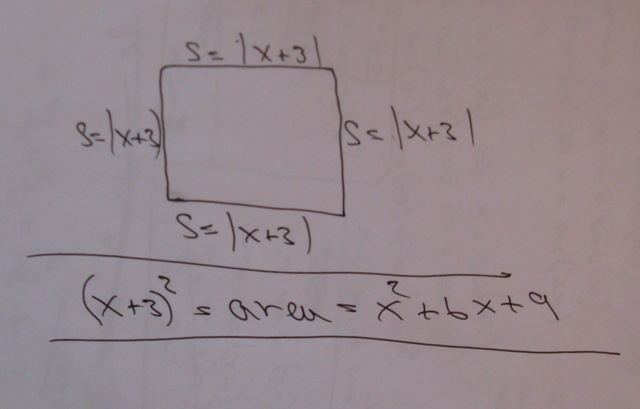
here's a picture of your square:
the length of each side in the square is equal to |x+3|.
this means each side in the square is equal to the absolute value of (x+3).
an example:
let x = -5.
each side of your square is equal to |-5+3| which is equal to |-2| which is equal to 2.
the area of your square is equal to x^2 + 6x + 9 after you replace x with (-5) to get (-5)^2 + 6*(-5) + 9 which is equal to 25 - 30 + 9 which is equal to 4.
since 2^4 = 4, the dimensions of each side and the area of the square confirm that the value of x = |-2| is good.
s is equal to 2
s^2 is equal to 4
Answer by richard1234(7193)   (Show Source): (Show Source):
You can put this solution on YOUR website! x^2 + 6x + 9 = (x+3)(x+3) = (-x-3)(-x-3).
The side of the length can be either x+3 or -x-3, depending on which one is positive. The best way to express it is |x+3|, so it is always positive (if x+3 is not zero).
Answer by ikleyn(53427)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A square has an area of x^2 + 6x + 9. Find the length of a side. Make a sketch of the square Please help
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Tutor @Theo' solution is many words.
I don't like toooo wordy solutions: I think that too wordy explanations are bad style to teach Math.
So, I will write another solution, much shorter and, I believe, more educative.
The expression x^2 + 6x + 9 represents an algebraic perfect square 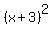 .
So, the area of the square is .
So, the area of the square is 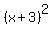 square units.
Hence, the side length of this square is square root of this perfect square square units.
Hence, the side length of this square is square root of this perfect square 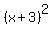 .
So, our first desire is to declare that the side length is (x+3) units.
But it would be too hastily and not always correct.
The reason is that this expression (x+3) can be negative, since we don't know what 'x' is.
Meanwhile, the length of the square must be positive due to the meaning of this notion/conception.
Therefore, more accurate is to write .
So, our first desire is to declare that the side length is (x+3) units.
But it would be too hastily and not always correct.
The reason is that this expression (x+3) can be negative, since we don't know what 'x' is.
Meanwhile, the length of the square must be positive due to the meaning of this notion/conception.
Therefore, more accurate is to write 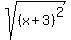 = |x+3| , using the absolute value.
This form is universally correct for all possible values of 'x'.
ANSWER. If the area of a square is x^2 + 6x + 9 square units, then the side of the square is |x+3| units. = |x+3| , using the absolute value.
This form is universally correct for all possible values of 'x'.
ANSWER. If the area of a square is x^2 + 6x + 9 square units, then the side of the square is |x+3| units.
Solved, with complete explanations in compact form.
|
|
|