Question 475562: Hello. I need to find an x such that <5,6> and <2,3x> are a)parallel, b)orthogonal, and c)neither. How do i do this?
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
You can put this solution on YOUR website!
<5,6> and <2,3x>
To be parallel one must be a multiple of the other:
<5,6> = k<2,3x>
<5,6> = <2k,3kx>
 For the first equation k =
For the first equation k =  Substitute in the second equation:
6 = 3(
Substitute in the second equation:
6 = 3( )x
12 = 3(5x)
12 = 15x )x
12 = 3(5x)
12 = 15x
 = x = x
 = x
--------------------------
<5,6> and <2,3x>
To be orthogonal their dot product must be 0:
<5,6>•<2,3x> = 0
(5)(2)+(6)(3x) = 0
10+18x = 0
18x = -10
x = = x
--------------------------
<5,6> and <2,3x>
To be orthogonal their dot product must be 0:
<5,6>•<2,3x> = 0
(5)(2)+(6)(3x) = 0
10+18x = 0
18x = -10
x = 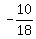 x =
x = 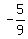 ----------------------------------
To be neither, choose x as anything other than those two values.
Edwin
----------------------------------
To be neither, choose x as anything other than those two values.
Edwin
|
|
|