Question 467184: please help me answer this question asap.
the measures of the consecutive sides of an isosceles trapezoid are 4:5:10:5. its height is 8, and its perimeter is 48. find the area of this trapezoid.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the following picture shows you what i am talking about.
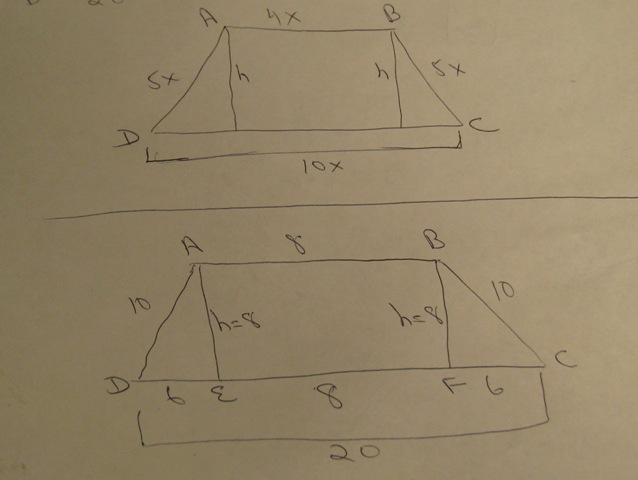
label your trapezoid ABCD starting from top left then to top right then to bottom right then to bottom left.
since this is an isosceles trapezoid, sides AB and CD are parallel, and sides AD and BC are congruent.
you are showing the ratio of the sides as 4:5:10:5
AB is assigned to 4
BC is assigned to 5
CD is assigned to 10
AD is assigned to 5
since these are ratios, and not actual sizes, then multiply each of them by a common factor which we'll call x.
the sides of your trapezoid are then equal to:
AB is equal to 4x
BC is equal to 5x
CD is equal to 10x
AD is equal to 5x
x is a common ratio that will apply to any size trapezoid with the sides in the same ratio.
you know that the height of the trapezoid is 8 and the perimeter is 48.
you want to find the area.
we can use the perimeter to find the sides of the trapezoid.
we just add up all the lengths of the sides and make them equal to 48 and solve for x.
you get:
4x + 5x + 10x + 5x = 48
combine like terms to get:
24x = 48
divide both sides of this equation by 24 to get:
x = 2
the lengths of your sides are now:
AB is equal to 8
BC is equal to 10
CD is equal to 20
AD is equal to 10
if you now drop a perpendicular from A to intersect with CD at E, and drop a perpendicular from B to intersect with CD at F, then you can find the area of the isosceles trapezoid.
AB is equal to 8
CD is equal to 20
dropping the perpendiculars from A and B to intersect with E and F on CD divides CD into 3 segments.
DE is equal to 6 and EF is equal to 8 and CF is equal to 6 making a total of 20 for the overall segment of CD.
you have now formed a right triangle of ADE with a right angle at E.
you have also formed a right triangle of BCF with a right angle at F.
the vertical lines are the altitudes (height) of the trapezoid.
since you know that the height of the trapezoid is 8, then the height of these altitudes is also 8.
to find the area of the trapezoid, use the formula A = 1/2 * (b1 + b2) * h
A is the area.
b1 and b2 are the smaller and the larger bases of the trapezoid..
h is the height.
b1 is equal to AB which is equal to 8.
b2 is equal to CD which is equal to 20.
h is equal to either AE or BF which are each equal to 8.
using these figures, the formula becomes:
A = 1/2 * (8 + 20) * 8 which becomes:
A = 1/2 * (28) * 8 which becomes:
A = 14 * 8 which becomes:
A = 112 square units.
|
|
|